Cách áp dụng kỹ thuật Self-Explanation trong SAT® Math để củng cố kiến thức

Nhiều người học có nền tảng kiến thức toán học khá tốt nhưng việc hiểu sâu bản chất bài toán và áp dụng linh hoạt các kỹ năng giải quyết vấn đề còn hạn chế. Hiện nay có nhiều phương pháp giúp cải thiện tư duy toán học khác nhau, và bài viết dưới đây sẽ hướng dẫn cách áp dụng kỹ thuật Self-Explanation để củng cố kiến thức toán SAT. Đây là kỹ thuật tự giải thích giúp người học củng cố kiến thức, phát hiện lỗi sai và tăng khả năng tư duy logic

Khó khăn trong quá trình học toán SAT

Mặc dù học sinh Việt Nam có nền tảng toán học khá vững vàng nhờ chương trình học phổ thông chú trọng luyện tập và tính toán, nhưng đối với SAT – một kỳ thi tiêu chuẩn quốc tế, nhiều người học gặp không ít trở ngại do những vấn đề sau:

Học công thức một cách máy móc

Nhiều học sinh có xu hướng học thuộc lòng các công thức và dạng bài mẫu thay vì hiểu được bản chất của bài toán. Điều này dẫn đến tình trạng người học chỉ biết áp dụng công thức mà không biết tại sao lại áp dụng như vậy. Do đó, người học dễ bị lúng túng khi đề bài thay đổi cách hỏi hoặc ẩn ý yêu cầu khác.

Tư duy một chiều, chưa có chiến lược linh hoạt

SAT Math không chỉ kiểm tra khả năng tính toán mà còn đánh giá năng lực suy luận và tư duy giải quyết vấn đề. Tuy nhiên, nhiều học sinh chưa được rèn luyện thói quen so sánh các phương pháp giải khác nhau để chọn cách tối ưu, kiểm tra lại tính logic của từng bước giải cũng như phân tích và loại trừ đáp án sai.

Thiếu khả năng phản biện và tự nhận diện lỗi sai

Sau khi làm bài, không ít người học chỉ đối chiếu kết quả với đáp án mà không dành thời gian xem lại tại sao mình làm sai. Thói quen này khiến người học lặp lại lỗi sai cũ do không nhận diện được gốc rễ vấn đề, từ đó khó cải thiện điểm số dù luyện đề nhiều.

Nhìn chung, những vấn đề trên bắt nguồn từ sự thiếu chủ động trong tư duy học và giải toán. Vì vậy, kỹ thuật Self-Explanation – tức tự diễn giải lại lý do và quá trình suy nghĩ trong khi giải bài – được xem là công cụ đơn giản nhưng hiệu quả để học sâu, học chắc và khắc phục các điểm yếu trong quá trình luyện thi SAT Math.

Tham khảo thêm: Học SAT mất bao lâu? Tổng quan về quá trình học và thi SAT

Phương pháp Self-Explanation là gì?

Self-explanation là một phương pháp tạo ra kiến thức mới mang tính cá nhân thông qua việc kết nối các kiến thức đã được cung cấp rõ ràng trước đó [1]. Thông thường, quá trình này có thể diễn ra một cách tự nhiên khi người học đọc các lời giải mẫu. Lý do là vì những lời giải này chỉ nêu các bước giải mà không giải thích rõ tại sao lại thực hiện từng bước đó. Điều này buộc người học phải tự suy nghĩ và tạo ra lời giải thích của riêng mình để thật sự hiểu rõ tư duy giải quyết bài toán.

Mặc dù self-explaining (tự giải thích) và explaining (giải thích cho người khác) đều là những hoạt động mang tính xây dựng trong học tập nhưng chúng khác nhau về bản chất [2]:

• Self-explaining là hoạt động nhận thức cá nhân, không nhất thiết phải được diễn đạt bằng lời. Nó xuất phát từ kiến thức nền sẵn có của chính người học.

• Explaining, ngược lại, là một hoạt động giao tiếp vì mục đích chính của nó là truyền đạt cho người khác hiểu. Do đó, người giải thích dựa trên hiểu biết của người nghe để chọn lọc, tổ chức thông tin sao cho dễ hiểu.

Tuy nhiên, self-explanation vẫn còn là một khái niệm khá tổng quát, chưa chỉ rõ người học cần tự giải thích ra sao hay dựa trên nguyên tắc nào. Một khái niệm cụ thể hơn là tự giải thích dựa trên nguyên lý/lý thuyết (principle-based self-explanation). Trong phương pháp này, người học tự giải thích các vấn đề thực tế dựa trên những nguyên lý, quy luật chung [3].

Thông qua việc tự giải thích nhiều trường hợp khác nhau, người học dần hình thành một cấu trúc tri thức, trong đó nguyên lý và các ví dụ cụ thể được kết nối chặt chẽ với nhau. Điều quan trọng là người học không chỉ biết rằng một bài toán có liên quan đến nguyên lý nào đó mà còn hiểu rõ chính xác nguyên lý được áp dụng như thế nào và ở bước nào của lời giải. Đồng thời, người học có thể xây dựng mối liên hệ giữa các khái niệm riêng lẻ, từ đó phát triển hiểu biết sâu sắc hơn.

Chằng hạn, khi giải một bài toán, người học cần tự giải thích được cần áp dụng công thức và cách giải nào, công thức đó dựa trên kiến thức cơ bản nào và vì sao có thể áp dụng để giải bài toán đó. Khi đó, người học không chỉ dừng lại ở việc thực hiện các bước giải theo khuôn mẫu mà thực sự hiểu được mối liên hệ giữa lý thuyết và ví dụ cụ thể.

Đọc thêm: Phương pháp giải các dạng bài trong SAT Math (P1)

Lợi ích của phương pháp Self-Explanation

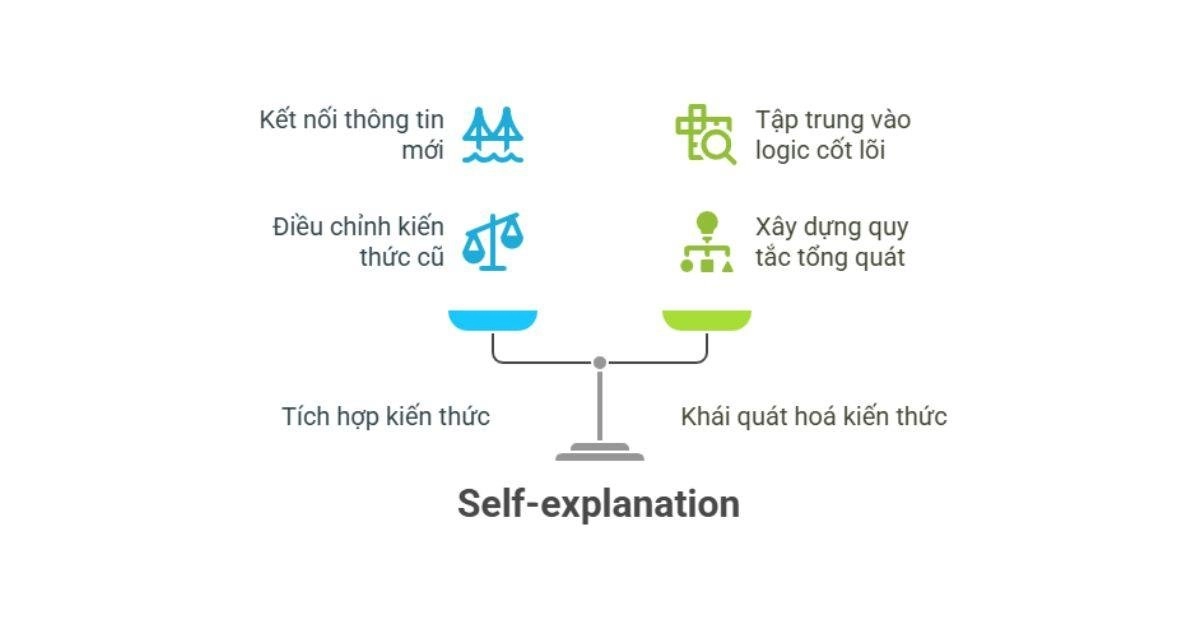
Self-explanation là phương pháp hỗ trợ quá trình học tập thông qua hai cơ chế chính [4]:

Tích hợp kiến thức

Khi tự diễn giải bài học cho bản thân, người học thường liên kết các thông tin mới lại với nhau hoặc kết nối chúng với kiến thức đã có. Bên cạnh đó, khi thông tin mới mâu thuẫn với kiến thức cũ, người học có cơ hội nhận diện mâu thuẫn đó và suy luận để điều chỉnh hiểu biết của mình. Quá trình tự giải thích cũng có thể giúp làm rõ những thông tin quan trọng mà người học đã bỏ qua hoặc hiểu sai lúc đầu.

Khái quát hoá kiến thức

Các nghiên cứu cho thấy việc tự tạo ra lời giải thích giúp người học tập trung vào đặc điểm logic, bản chất của nội dung bài học. Nhờ đó, người học có thể nhận ra các nguyên lý tổng quát ẩn sau các bước giải, nhận ra các đặc điểm cốt lõi của ví dụ mẫu và từ đó xây dựng được quy tắc hoặc chiến lược giải phù hợp với nhiều dạng bài khác nhau.

Tìm hiểu thêm: SAT Math formulas - Tổng hợp các công thức thường gặp trong SAT Math

Khi nào nên áp dụng Self-Explanation?

Quá trình học tập bao gồm nhiều giai đoạn khác nhau và người học cần cân nhắc lựa chọn phương pháp học tập phù hợp trong mỗi giai đoạn đó. Nhìn chung người học tiếp thu và vận dụng kiến thức, kỹ năng mới theo 3 giai đoạn bao gồm [5]:

• Giai đoạn đầu: Người học tìm hiểu để hiểu những nguyên lý cơ bản của lĩnh vực mà chưa cần áp dụng chúng. Ở giai đoạn này, họ chủ yếu đọc tài liệu và học lý thuyết.

• Giai đoạn giữa: Người học bắt đầu học cách vận dụng các nguyên lý vào giải quyết vấn đề cụ thể, thường thông qua nghiên cứu các ví dụ mẫu. Hoạt động tự giải thích trong giai đoạn này đóng vai trò quan trọng giúp củng cố hiểu biết.

• Giai đoạn sau: Người học luyện tập để tăng tốc độ và độ chính xác. Lúc này, giải bài tập thực tế giữ vai trò quan trọng hơn.

Như vậy, phương pháp tự giải thích đặc biệt hiệu quả ở giai đoạn trung gian, khi người học bắt đầu chuyển từ học lý thuyết sang vận dụng vì nó giúp người học hiểu sâu về nguyên lý và mối liên hệ giữa lý thuyết với cách áp dụng. Tuy nhiên, ở các giai đoạn sau, việc tiếp tục tự giải thích có thể trở nên dư thừa, tốn thời gian và không còn mang lại hiệu quả rõ rệt. Nhiều nghiên cứu cũng chỉ ra rằng tự giải thích mang lại lợi ích rõ rệt hơn cho người học ở trình độ cơ bản, tức là những người đang trong giai đoạn đầu của quá trình hình thành kỹ năng. Ngược lại, nếu người học đã quen thuộc với các khái niệm tương tự từ trước, hoạt động này không còn giúp cải thiện kết quả học tập đáng kể.

Tóm lại, việc khuyến khích người học tự giải thích là rất cần thiết trong giai đoạn đầu để xây dựng nền tảng hiểu biết vững chắc. Nhưng khi đã nắm vững nguyên lý và biết vận dụng linh hoạt, người học nên chuyển sang luyện tập nhằm giải quyết các bài toán thành thạo hơn.

Tham khảo: Advanced Math trong SAT Math - Cách làm bài, bài tập ví dụ và luyện tập

Áp dụng kỹ thuật Self-Explanation để củng cố kiến thức toán SAT

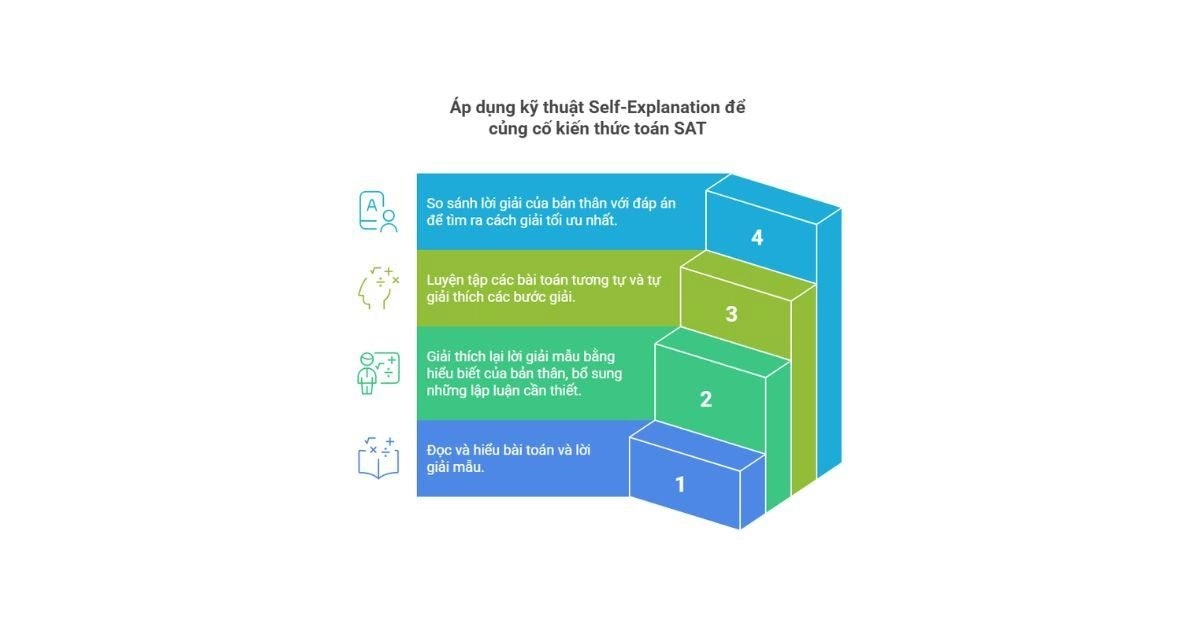
Bước 1: Đọc bài tập và lời giải mẫu

Khi bắt đầu luyện tập một dạng bài mới, người học cần đọc kỹ đề bài, sau đó quan sát từng bước giải trong lời giải mẫu. Tuy nhiên, thay vì chỉ đọc để "chép lại cách làm", người học cần tập trung vào việc:

• Tìm hiểu lý do tại sao từng bước giải được thực hiện như vậy.

• Nhận diện kiến thức nào được sử dụng (ví dụ: công thức, định lý, khái niệm toán học).

• Phát hiện những gì chưa được giải thích rõ trong lời giải mẫu.

Bước 2: Tự giải thích lại bài mẫu

Sau khi hiểu rõ ý nghĩa của từng bước và bổ sung những lập luận không được thể hiện trong lời giải, người học tiến hành giải thích lại toàn bộ quá trình suy luận và tính toán để giải quyết bài tập đó. Người học có thể tự giải thích theo nhiều cách khác nhau như viết giấy hoặc nói thành lời.

Khi viết giấy, người học có thể lập sơ đồ dựa trên các giả thiết đã cho, mô tả mối liên hệ giữa các giả thiết đó, thông tin nào là dấu hiệu cho biết cần sử dụng kiến thức toán học nào, dẫn đến kết quả ra sao. Sơ đồ hoàn chỉnh thể hiện quá trình tư duy, suy luận bài toán.

Đối với phương pháp tự giải thích bằng lời nói, người học đóng vai trò như một người hướng dẫn của chính mình, qua đó giải thích cặn kẽ từng bước làm bài. Bên cạnh đó, thay vì chỉ diễn giải liên tục bằng hình thức tường thuật, người học có thể tự đặt ra các câu hỏi như “Vì sao mình cần dùng công thức này?”, “Có dữ kiện nào chưa dùng đến không?”,…

Mỗi cách học sẽ phù hợp với phong cách học tập của mỗi người — yên tĩnh hoặc sinh động. Người học cũng có thể kết hợp cả hai phương pháp để ghi nhớ rèn luyện tư duy tốt hơn.

Bước 2: Luyện tập phân tích và tự giải thích các dạng bài tương tự

Người học cần luyện tập nhiều dạng bài tương tự để củng cố kiến thức tốt hơn. Đối với bước này, người học không cần tự giải thích chi tiết như bài mẫu, tuy nhiên vẫn cần ghi chú quá trình suy luận của bản thân đễ dễ đối chiếu với đáp án và xem lại khi cần ôn tập.

Bước 4: Đối chiếu cách giải của bản thân với đáp án

Người học đối chiếu câu trả lời và cách giải của mình với đáp án và lời giải mẫu (nếu có). Đối với những câu trả lời đúng, người học so sánh hai cách giải để tìm ra điểm giống và khác nhau, từ đó xác định đâu là cách giải phù hợp hay tiết kiệm thời gian hơn. Đối với những câu trả lời sai, người học so sánh hai cách giải để xác định lỗi của bản thân, sau đó viết lại cách giải đúng và tự giải thích lại để thật sự hiểu rõ cách giải.

Ví dụ:

A small bakery makes loaves of sourdough bread.

• The fixed costs (equipment, rent, electricity, etc.) are $120 per day.

• The cost of ingredients and labor for each loaf is $1.20.

• The bakery sells each loaf for $3.00.

a) How many loaves must the bakery sell in a day to break even (earn no profit or loss)?

b) If the bakery wants to make at least $150 in profit per day, how many loaves must it sell?

Phân tích đề:

Đề bài đưa ra những dữ kiện gì?

• Chi phí đầu vào bao gồm: phí cố định $120/ngày và phí thay đổi theo số lượng bánh $1.20/ổ

• Chi phí đầu ra là giá tiền mỗi ổ bánh: $3.00/ổ

Những giá trị này có ý nghĩa gì?
→ Tính toán chi phí đầu vào và đầu ra sẽ kết luận được lợi nhuận của tiệm bánh (Lợi nhuận = Doanh thu — Chi phí).

Đề bài yêu cầu tính toán gì?

• Break even (earn no profit or loss): Cần bán nhiêu bánh để hoà vốn, nghĩa là mức thu bằng với mức chi.

• At least $150 in profit: Cần bán nhiêu bánh để lời $150, nghĩa là mức thu cao hơn mức chi $150.

Giải bài toán này bằng cách nào?
→ Bài toán yêu cầu tìm số lượng bánh và có nhiều dữ kiện xoay quanh biến số này. Do đó có thể đặt số lượng bánh là x và lập các phương trình để tìm x.

Giải chi tiết:

Gọi x là số ổ bánh bán mỗi ngày.

Khi đó:

• Chi phí nguyên liệu và nhân công là 1.2x. Tổng chi phí mỗi ngày là 120 + 1.2x

• Doanh thu mỗi ngày là 3x

Lợi nhuận = Doanh thu — Chi phí = 3x — 120 — 1.2x = 1.8x — 120.

a) Hoà vốn: 1.8x — 120 = 0 → x = 66.7 → Cần bán 67 ổ bánh.

b) Lời $150: 1.8x — 120 \(\ge\)150 → x \(\ge\)150 → Cần bán ít nhất 150 ổ bánh.

Phản biện:

Kết quả này đã đúng chưa?

Người học kiểm tra đáp án bằng cách thử lại đáp án:

• Khi bán 67 ổ bánh, chi phí là $120 + $1.2×67 = $200.4, doanh thu là $201 → Đủ hoà vốn.

• Khi bán 150 ổ bánh, chi phí là $120 + $1.2×150 = $300, doanh thu là $450→ Lợi nhuận là $150.

→ Bài toán đã được giải đúng.

Lưu ý

Để quá trình học bằng phương pháp tự giải thích hiệu quả hơn, người học cần lưu ý những điểm sau:

Phân biệt rõ self-explanation với paraphrasing và monitoring

Nhiều người học cho rằng chỉ cần nhắc lại bài giải theo cách khác (paraphrasing) hoặc kiểm tra mình có hiểu lời giải hay không (monitoring) là đã “tự giải thích”. Tuy nhiên, paraphrasing chỉ đơn thuần là lặp lại lời giải mẫu bằng cách diễn đạt lại, không làm rõ mối quan hệ giữa các bước giải với kiến thức nền, còn monitoring chỉ giúp theo dõi tiến độ làm bài, nhưng không đi sâu vào “vì sao mình làm như vậy”.

Thay vào đó, người học cần đặt nhiều câu hỏi và giải đáp để làm rõ vấn đề như:

• Vì sao bước này đúng?

• Công thức này áp dụng được trong điều kiện nào?

• Nếu điều kiện thay đổi, cách giải còn đúng không?

Tự giải thích cả lời giải đúng và sai

Theo lý thuyết kiến thức phủ định (negative knowledge), việc biết rõ điều gì là sai cũng có giá trị, vì nó giúp người học nhận diện và tránh mắc lại lỗi [6]. Tuy nhiên, “kiến thức sai” cần được liên kết với kiến thức đúng tương ứng để người học hiểu sâu và ứng dụng chính xác hơn. Vì vậy, việc người học tự giải song song các lời giải đúng và lời giải sai có thể nâng cao hiệu quả học tập. Khi giải thích câu trả lời sai, người học cần tìm ra lỗi và tìm hiểu nguyên nhân, thiếu sót nào có thể dẫn đến lỗi đó để tránh lặp lại tương tự.

Không nên phụ thuộc quá nhiều vào bài giải mẫu

Người học có thói quen đọc kỹ lời giải mẫu trước, sau đó mới bắt đầu tự giải thích. Tuy nhiên, việc đọc trước lời giải mẫu chỉ nên được thực hiện khi người học bắt đầu làm quen với dạng bài mới. Việc luôn đọc trước lời giải gây hạn chế khả năng tư duy độc lập của người học, dẫn đến nhiều trở ngại khi làm bài thi thực tế. Người học cần tự giải thích và làm bài trước, sau đó kiểm tra đáp án, tự tìm lỗi sai và cuối cùng là đọc lời giải mẫu và tự giải thích lại một cách hoàn chỉnh.

Cần đặt câu hỏi phản biện

Self-explanation hiệu quả không chỉ là diễn giải, mà cần phản biện lại chính cách giải của mình. Câu hỏi phản biện giúp phát hiện lỗi sai ngầm, hiểu nhầm hoặc phương pháp giải chưa tối ưu. Ngược lại, thiếu tư duy phản biện trong cách giải thích khiến người học dễ lặp lại lỗi sai trong các dạng bài tương tự.

Ví dụ các câu hỏi phản biện cần có:

• Có cách giải nào ngắn hơn không?

• Nếu bài toán cho thêm yếu tố X thì mình sẽ làm thế nào?

• Tại sao không chọn cách giải Y?

• Liệu có thể rút gọn bước này không?

Tham khảo thêm: Những lưu ý quan trọng mà người học cần biết khi tham gia kì thi SAT

Tổng kết

Bài viết trên đã giới thiệu khái niệm và trình bày cách áp dụng kỹ thuật Self-Explanation để củng cố kiến thức toán SAT. Đây không phải là một phương pháp học tập mới nhưng rất phù hợp với yêu cầu tư duy logic và phân tích của bài thi này và đặc biệt hiệu quả đối với những người bắt đầu học. Khi tự giải thích từng bước làm và lý do lựa chọn cách giải, người học không chỉ hiểu sâu bản chất kiến thức, mà còn phát triển tư duy phản biện, khả năng tự học và tự kiểm soát quá trình tư duy, giúp nâng cao hiệu quả ôn luyện và đạt kết quả tốt hơn trong bài thi.

Kỳ thi SAT Digital đòi hỏi sự chuẩn bị kỹ lưỡng và chiến lược học tập hiệu quả. Khóa học SAT Comprehensive tại ZIM mang đến cho học viên trải nghiệm giáo dục cá nhân hóa với hơn 1.000 biến thể giáo trình độc quyền, giúp phát triển toàn diện các kỹ năng Toán, Đọc hiểu và Viết - những thành phần chính của kỳ thi SAT Digital 2025. Thông qua khoá học SAT được thiết kế phù hợp cho từng học viên, người học sẽ được chuẩn bị đầy đủ cho hình thức thi thích ứng (Adaptive Testing). Liên hệ Hotline 1900-2833 (nhánh số 1) để được tư vấn chi tiết.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.