PEMDAS là gì? Quy tắc cơ bản giúp chinh phục các bài toán SAT® Math
Key takeaways
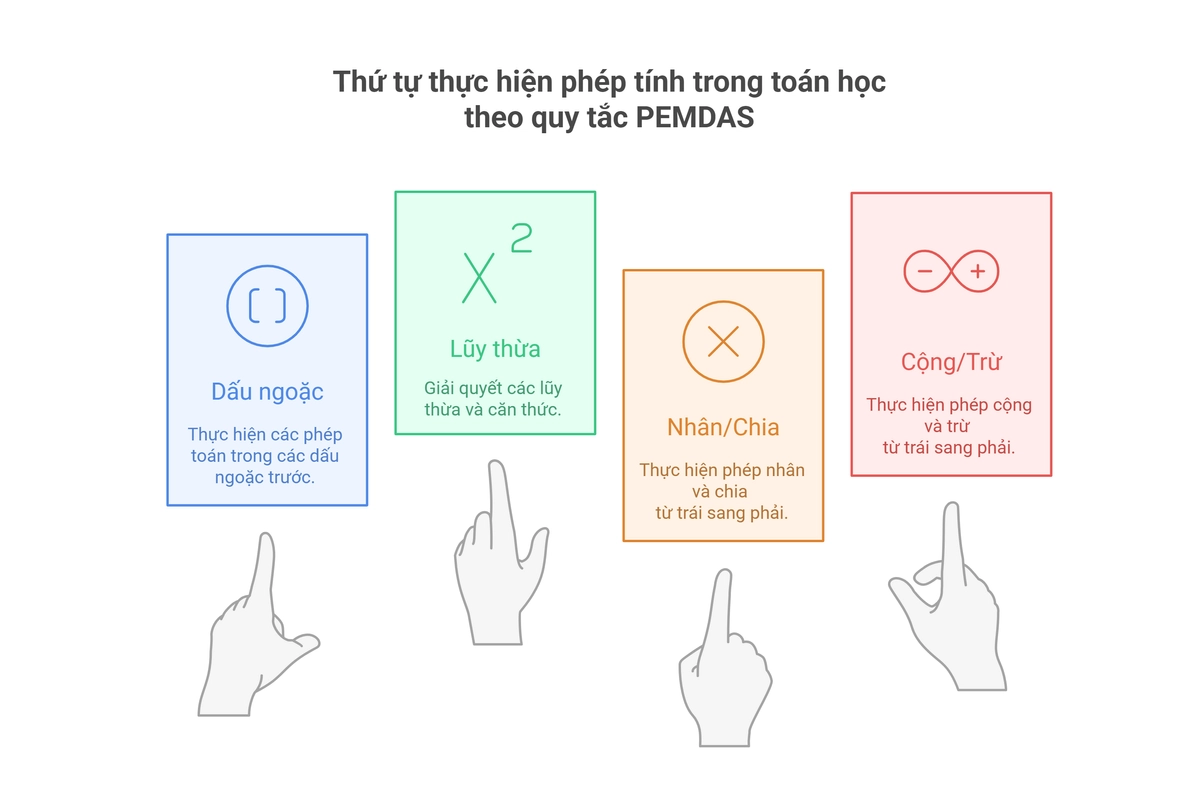
Quy tắc PEMDAS thể hiện thứ tự thực hiện phép tính đúng theo quy chuẩn trong toán học để đảm bảo tính chính xác và thống nhất của đáp án:
P (Parentheses) đại diện cho dấu ngoặc [{( )}].
E (Exponents) đại diện cho lũy thừa và căn bậc hai, ba.
MD (Multiplication/ Division) đại diện cho phép nhân (×) và chia (÷).
AS (Addition/ Subtraction) đại diện cho phép cộng (+) và trừ (-).
SAT (Scholastic Aptitude Test hay Scholastic Assessment Test) là bài thi chuẩn hóa dùng để đánh giá năng lực đọc, viết và toán tiếng Anh của thí sinh và được sử dụng rộng rãi trong xét tuyển đại học hay cao học ở Mỹ. Trong đó, phần SAT Math (toán tiếng Anh) có thể gây khó khăn cho không ít thí sinh khi mới tiếp cận và ôn luyện các dạng bài này.
Do đó, bài viết sau đây của ZIM sẽ giới thiệu về một quy tắc nền tảng trong SAT Math - PEMDAS (viết tắt của Parentheses, Exponents, Multiplication/Division, Addition/Subtraction). Đây là quy tắc chuẩn quốc tế về thứ tự thực hiện phép tính, qua đó giúp thí sinh rèn luyện được tư duy chiến lược để xử lý các bài toán một cách tự tin, nhanh chóng và chính xác để đạt điểm Math 700+, tránh những lỗi “đáng tiếc” do tính toán sai thứ tự và tối ưu hóa thời gian làm bài.
PEMDAS là gì?
Trong toán học, khi giải một biểu thức có nhiều phép tính khác nhau, thí sinh cần tuân theo một thứ tự phép tính chuẩn để đảm bảo kết quả chính xác và tính nhất quán khi giải các bài toán khác nhau. Thứ tự này được gọi là quy tắc PEMDAS.
Trong quy tắc PEMDAS, mỗi chữ cái đại diện cho một phép tính trong toán học và thứ tự của các chữ cái này chính là trình tự hệ thống giúp các thí sinh biết chính xác phép nào cần thực hiện trước khi giải biểu thức và tránh các lỗi có thể xảy ra do thực hiện phép tính sai thứ tự. [1]

Các chữ cái trong PEMDAS lần lượt đại diện cho [1]:
Parentheses (Dấu ngoặc): Thực hiện các phép tính trong dấu ngoặc đơn ( ), dấu ngoặc vuông [ ], hay dấu ngoặc nhọn { } trước. Với các ngoặc lồng vào nhau, làm từ trong ra ngoài.
Exponents (Lũy thừa): Giải quyết các biểu thức có lũy thừa hoặc căn bậc hai, căn bậc ba.
Multiplication/ Division (Nhân/ Chia): Thực hiện phép nhân và phép chia theo thứ tự từ trái sang phải. Cả hai có mức ưu tiên ngang nhau.
Addition/ Subtraction (Cộng/ Trừ): Thực hiện các các phép cộng và phép trừ theo thứ tự từ trái sang phải. Cả hai có mức ưu tiên ngang nhau.
Thí sinh cần lưu ý rằng quy tắc PEMDAS không có nghĩa là luôn luôn phải thực hiện phép nhân trước phép chia, hay phép cộng trước phép trừ. Phép nhân và phép chia có độ ưu tiên ngang nhau, và cần thực hiện theo thứ tự xuất hiện từ trái sang phải. Điều tương tự được áp dụng với phép cộng và phép trừ. Đây có thể là điểm then chốt giúp thí sinh tránh các “bẫy” tính toán trong đề thi SAT.
Xem thêm: Simplifying Expressions - Cách đơn giản hóa biểu thức đại số
Giải thích chi tiết từng bước theo PEMDAS
Bước 1: Parentheses - Dấu ngoặc
Đây là bước đầu tiên. Nhiệm vụ của thí sinh là rút gọn bất kỳ biểu thức nào nằm trong các dấu ngoặc bao gồm dấu ngoặc đơn ( ), dấu ngoặc vuông [ ] và dấu ngoặc nhọn { } trước khi thực hiện các phép toán bên ngoài. Khi có các dấu ngoặc lồng nhau (nested parentheses), thí sinh cần bắt đầu từ cặp ngoặc trong cùng và làm dần ra ngoài.
Ví dụ: \([(10−2)×3]+5\)
Đầu tiên, giải quyết cặp ngoặc trong cùng: \((10−2)=8\)
Biểu thức trở thành \([8×3]+5\)
Tiếp theo, giải quyết cặp ngoặc vuông: \([8×3]=24\)
Biểu thức trở thành \(24+5\)
Cuối cùng, thực hiện phép cộng: \(24+5=29\)
Bước 2: Exponents - Lũy thừa
Khi tất cả các dấu ngoặc đã được xử lý, bước tiếp theo là tính toán tất cả các lũy thừa. Điều này cũng áp dụng cho căn bậc hai và căn bậc ba, vì căn thức thực chất là một dạng lũy thừa có số mũ phân số.
Ví dụ: \(2^3+\sqrt{25}\)
Biểu thức không bao gồm dấu ngoặc nào nên thí sinh tiến tới bước tiếp theo là lũy thừa và căn bậc hai.
Đầu tiên, giải quyết lũy thừa và căn bậc hai: \(2^3=8\) và \(\sqrt{25}=5\)
Biểu thức trở thành \(8+5\)
Cuối cùng, thực hiện phép cộng: \(8+5=13\)
Bước 3: Multiplication/ Division - Nhân/ Chia
Đây là nơi không ít thí sinh mắc lỗi hoặc dính “bẫy”. Phép nhân không phải lúc nào cũng thực hiện trước phép chia. Chúng có mức độ ưu tiên như nhau và thí sinh cần hực hiện phép nhân/chia theo thứ tự xuất hiện từ trái sang phải.
Ví dụ: \(12÷2×3\)
Biểu thức chỉ gồm phép nhân và chia (mức ưu tiên ngang nhau) nên cần thực hiện từ trái sang phải.
Thực hiện phép chia: \(12÷2=6\)
Biểu thức trở thành \(6×3\)
Tiếp đến, thực hiện phép nhân: \(6×3=18\)
Bước 4: Addition/ Subtraction - Cộng/ Trừ
Tương tự như phép nhân và chia, phép cộng và phép trừ có cùng mức độ ưu tiên. Thí sinh cần thực hiện chúng theo thứ tự xuất hiện từ trái sang phải để có được đáp án chính xác và tránh mắc “bẫy” của đề thi.
Ví dụ: \(15−5+10\)
Biểu thức chỉ gồm phép cộng và trừ (mức ưu tiên ngang nhau) nên cần thực hiện từ trái sang phải.
Thực hiện phép trừ: \(15-5=10\)
Biểu thức trở thành \(10+10\)
Tiếp đến, thực hiện phép cộng: \(10+10=20\)
Bằng cách nắm vững bốn bước này và quy tắc từ trái sang phải đối với phép nhân/chia và phép cộng/trừ, thí sinh sẽ xây dựng được một nền tảng vững chắc để xử lý bất kỳ biểu thức đại số phức tạp nào trong đề thi SAT.
Một số lưu ý khi áp dụng quy tắc PEMDAS
Thanh phân số chứa dấu ngoặc ngầm
Trong một biểu thức phân số, thanh phân số có tác dụng nhóm toàn bộ tử số và mẫu số. Điều này có nghĩa là thí sinh phải hoàn thành việc rút gọn toàn bộ tử số và toàn bộ mẫu số trước khi thực hiện phép chia cuối cùng.
Ví dụ: \(\frac{10+2}{2\times3}\)
Rút gọn tử số: \(10+2=12\)
Rút gọn mẫu số: \(2\times3=6\)
Cuối cùng, thực hiện phép chia: \(\frac{12}{6}=2\)
Dấu nhân ngầm
Trong toán học, khi một số đứng liền kề với một dấu ngoặc hoặc một biểu thức khác mà không có dấu phép toán nào ở giữa, đó mặc định là phép nhân.
Ví dụ: \(11+2(-2)=11+[2\times(-2)]=11+(-4)=7\)
Đọc thêm: SAT Math formulas - Tổng hợp các công thức thường gặp trong SAT Math
Minh họa ví dụ cụ thể áp dụng PEMDAS trong bài toán SAT
Ví dụ 1: Biểu thức có dấu ngoặc, phân số, lũy thừa và các phép tính hỗn hợp
\[\frac{\left(6+2\right)^2}{4}+3\times\left(5-2^2\right)\]Để rút gọn biểu thức trên, thí sinh cần dựa vào thứ tự ưu tiên theo quy tắc PEMDAS (dấu ngoặc → lũy thừa → nhân/chia → cộng/trừ)
Bước 1: Xử lý dấu ngoặc
Theo quy tắc PEMDAS, cần bắt đầu giải các phép tính trong ngoặc:
Ngoặc thứ nhất: \((6+2)=8\)
Ngoặc thứ hai: \(\left(5-2^2\right)\)
Tiếp tục áp dụng quy tắc PEMDAS để giải phép toán bên trong ngoặc thứ hai:
Xử lý lũy thừa trước: \(2^2=4\)
Xử lý tiếp đến phép trừ: \(5-4=1\)
Do đó, ngoặc thứ hai: \(\left(5-2^2\right)=1\)
=> Lúc này, biểu thức được rút gọn thành: \(\frac{8^2}{4}+3\times1\)
Bước 2: Xử lý lũy thừa
Theo quy tắc PEMDAS, sau khi đã xử lý xong ngoặc, tiếp tục xử lý lũy thừa.
Lũy thừa còn lại trong biểu thức: \(8^2=64\)
=> Lúc này, biểu thức được rút gọn thành: \(\frac{64}{4}+3\times1\)
Bước 3: Xử lý phép nhân/chia
Bước tiếp theo trong quy tắc PEMDAS là xử lý phép nhân và chia. Thanh phân số đóng vai trò là phép chia và các phép nhân/chia có mức độ ưu tiên ngang nhau nên được thực hiện theo trình tự từ trái sang phải.
Thực hiện phép chia: \(\frac{64}{4}=16\)
Thực hiện phép nhân: \(3\times1=3\)
=> Lúc này, biểu thức được rút gọn thành: \(16+3\)
Bước 4: Xử lý phép cộng/trừ
Bước cuối cùng trong quy tắc PEMDAS là xử lý phép cộng và trừ theo thứ tự từ trái sang phải.
Thực hiện phép cộng còn lại: \(16+3=19\)
=> Đáp án cuối cùng sau khi rút gọn biểu thức đã cho là 19.
Ví dụ 2: Biểu thức phức tạp có ngoặc lồng và nhiều phép toán xen kẽ
\[\sqrt{36}-2\left\lbrack3^2-\left(4+2\right)\times\frac63\right\rbrack\]Để rút gọn biểu thức trên, thí sinh cần dựa vào thứ tự ưu tiên theo quy tắc PEMDAS (dấu ngoặc → lũy thừa → nhân/chia → cộng/trừ).
Bước 1: Xử lý dấu ngoặc
Theo quy tắc PEMDAS, cần bắt đầu với các phép tính trong ngoặc, nếu có nhiều ngoặc lồng vào nhau thì thực hiện từ ngoặc trong đến ngoặc ngoài.
Xử lý ngoặc tròn bên trong: \((4+2)=6\)
Ngoặc vuông bên ngoài trở thành: \([3^2-6\times\frac63]\)
Tiếp tục áp dụng quy tắc PEMDAS để giải các phép toán bên trong ngoặc vuông.
Xử lý lũy thừa: \(3^2=9\)
Biểu thức trở thành: \([9-6\times\frac63]\)
Xử lý phép nhân/chia: \(6\times\frac63=12\)
Biểu thức trở thành: \([9-12]\)
Cuối cùng, thực hiện phép trừ: \(9-12=-3\)
Do đó, ngoặc vuông bên ngoài: \([3^2-6\times\frac63]=-3\)
=> Lúc này, toàn bộ biểu thức được rút gọn thành: \(\sqrt{36}-2[-3]\)
Bước 2: Xử lý lũy thừa
Theo quy tắc PEMDAS, sau khi đã xử lý xong ngoặc, tiếp tục xử lý lũy thừa. Vì căn thức thực chất là một dạng lũy thừa có số mũ phân số, nên tiếp đến sẽ xử lý căn bậc hai có trong biểu thức được rút gọn.
Xử lý căn bậc hai: \(\sqrt{36}=6\)
=> Lúc này, toàn bộ biểu thức được rút gọn thành: \(6-2[-3]\)
Bước 3: Xử lý phép nhân/chia
Bước tiếp theo trong quy tắc PEMDAS là xử lý phép nhân và chia. Ngoài ra, cần lưu ý rằng một số đứng cạnh dấu ngoặc đại diện cho phép nhân và các phép nhân/chia được thực hiện từ trái sang phải.
Thực hiện phép nhân: \(2[−3]=2×(−3)=−6\).
=> Lúc này, toàn bộ biểu thức được rút gọn thành: \(6−(-6)\)
Bước 4: Xử lý phép cộng/trừ
Bước cuối cùng trong quy tắc PEMDAS là xử lý phép cộng và trừ theo thứ tự từ trái sang phải. Bên cạnh đó, cần lưu ý rằng phép trừ một số âm tương đương với phép cộng.
Thực hiện phép trừ còn lại: \(6−(-6) = 6+6=12\)
=> Đáp án cuối cùng sau khi rút gọn biểu thức đã cho là 12.
Đọc thêm: Essential Vocab for SAT® Math - Algebra | Unit 1: Total and Corresponding
Bài tập vận dụng

Bài tập 1
If \(y=3\sqrt{x+1}-2\), what is the value of y when x = 8?
A) 7
B) 4
C) -1
D) -4
Đáp án và giải thích:
Bài toán yêu cầu tìm giá trị của y khi thay x = 8 vào biểu thức.
Đầu tiên, thay giá trị x = 8 vào biểu thức: \(y=3\sqrt{8+1}-2\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức:
Exponents (Lũy thừa): Xử lý căn bậc hai:
\(\sqrt{8+1}=\sqrt9=3\)
—> Biểu thức trở thành: \(y = 3(3) - 2\)
Multiplication (Nhân): Thực hiện phép nhân ngầm: \(3 \times 3 = 9\)
—> Biểu thức trở thành: \( y = 9 - 2\)
Subtraction (Trừ): Thực hiện phép trừ: \(9 - 2 = 7\)
=> Đáp án: A) 7
Bài tập 2
If \(y=\frac{\left(x-3\right)^2}{2}+5\) and x = 7, what is the value of y?
A) 11
B) 13
C) 15
D) 17
Đáp án và giải thích:
Bài toán yêu cầu tìm giá trị của y khi thay x = 7 vào biểu thức.
Đầu tiên, thay giá trị x = 7 vào biểu thức: \(y=\frac{(7-3)^2}{2}+5\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức:
Parentheses (Dấu ngoặc): Xử lý phép tính trong ngoặc: 7 - 3 = 4
—> Biểu thức trở thành: \( y = \frac{4^2}{2} + 5\)
Exponents (Lũy thừa): Xử lý lũy thừa: \(4^2 = 16\)
—> Biểu thức trở thành: \(y = \frac{16}{2} + 5\)
Division (Chia): Thanh phân số có vai trò là phép chia, thực hiện phép chia: \(\frac{16}{2} = 8\)
—> Biểu thức trở thành: \(y = 8 + 5\)
Addition (Cộng): Thực hiện phép cộng: 8 + 5 = 13.
=> Đáp án: B) 13
Bài tập 3
Given \(f\left(x\right)=x^2-2x+1\). If x = 4, what is the value of f(x)?
A) 5
B) 7
C) 9
D) 11
Đáp án và giải thích:
Bài toán yêu cầu tìm giá trị của hàm số f(x) khi x = 4.
Đầu tiên, thay giá trị x = 4 vào hàm số: \( f(4) = 4^2 - 2(4) + 1\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức: \(4^2-2(4)+1\)
Exponents (Lũy thừa): Xử lý lũy thừa: \(4^2 = 16\)
—> Biểu thức trở thành: \(16-2(4)+1\)
Multiplication (Nhân): Thực hiện phép nhân: \(2(4) = 8\)
—> Biểu thức trở thành: 16 - 8 + 1
Addition/Subtraction (Cộng/Trừ): Thực hiện các phép tính từ trái sang phải: 16 - 8 = 8, sau đó 8 + 1 = 9.
=> Đáp án: C) 9
Bài tập 4
Given \(f(x)=(x-1)^3-2(x+3)\). If x = 2, what is the value of f(x)?
A) -3
B) 0
C) -9
D) 7
Đáp án và giải thích:
Bài toán yêu cầu tìm giá trị của hàm số f(x) khi x = 2.
Đầu tiên, thay giá trị x = 2 vào hàm số: \(f(2)=(2-1)^3-2(2+3)\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức: \((2-1)^3-2(2+3)\)
Parentheses (Dấu ngoặc): Xử lý phép tính trong ngoặc
Ngoặc thứ nhất: (2 − 1) = 1
Ngoặc thứ hai: (2 + 3) = 5
—> Biểu thức trở thành: \(1^3-2(5)\)
Exponents (Lũy thừa): Xử lý lũy thừa:
\(1^3=1\)
—> Biểu thức trở thành: 1 − 2(5)
Multiplication (Nhân): Thực hiện phép nhân:
2(5)=10
—> Biểu thức trở thành: 1 − 10
Subtraction (Trừ): Thực hiện phép trừ: 1 − 10 = −9
=> Đáp án: C) -9
Bài tập 5
If \(g\left(x\right)=\frac{x^2-4x}{2}+5\) and \(f\left(x\right)=2x-1\), what is the value of g(f(2))?
A) 4
B) 4.5
C) 3
D) 3.5
Đáp án và giải thích:
Đây là một bài toán hàm hợp, thí sinh cần làm từng bước từ giải hàm f(2) đến giải hàm g(f(2)).
Bước 1: Tính f(2)
Đầu tiên, thay giá trị x = 2 vào hàm f(x): \(f(2) = 2(2) - 1\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức: \(2(2)-1\)
Multiplication (Nhân): Thực hiện phép nhân: 2(2) = 4.
Subtraction (Trừ): Thực hiện phép trừ: 4 - 1 = 3.
Vậy, f(2) = 3.
Bước 2: Tính g(f(2)) hay g(3)
Đầu tiên, vì f(2) = 3 vào hàm g(f(2)) là hàm \(g(3) = \frac{3^2 - 4(3)}{2} + 5\)
Tiếp theo, áp dụng quy tắc PEMDAS để tìm giá trị của biểu thức: \(\frac{3^2 - 4(3)}{2}+5\)
Parentheses (Dấu ngoặc): Xử lý phép tính trong tử số (chứa ngoặc ngầm) theo quy tắc PEMDAS: \(3^2-4(3)=9-4\left(3\right)=9-12=-3\)
—> Biểu thức trở thành: \(\frac{-3}{2}+5\)
Division (Chia): Thanh phân số có vai trò là phép chia, thực hiện phép chia: \(\frac{-3}{2}=-1.5\)
—> Biểu thức trở thành: -1.5 + 5
Addition (Cộng): Thực hiện phép cộng:
-1.5 + 5 = 3.5
=> Đáp án: D) 3.5
Đọc tiếp: SAT Math Question - Khái niệm đại số, giải phương trình & hàm số
Tổng kết
Quy tắc PEMDAS (viết tắt của Parentheses, Exponents, Multiplication/Division, Addition/Subtraction) là nền tảng cốt lõi và nguyên lý cơ bản của toán học. Việc tuân thủ trình tự ngoặc → lũy thừa → nhân/chia → cộng/trừ sẽ giúp thí sinh có hướng tiếp cận chính xác nhằm giải quyết các dạng biểu thức SAT Math từ cơ bản đến nâng cao.
Khi nắm vững quy tắc này, thí sinh có thể có chiến lược giải bài hiệu quả, tiết kiệm thời gian và đảm bảo độ chính xác của câu trả lời. Do đó, thí sinh cần chủ động luyện tập với nhiều dạng bài khác nhau cho đến khi thứ tự các phép toán trong quy tắc PEMDAS trở thành phản xạ tự nhiên nếu muốn hướng đến mục tiêu điểm số cao hơn.
Để chinh phục bài thi SAT Digital, thí sinh cần trang bị tư duy logic và chiến lược giải toán hiệu quả. “Think in SAT Digital Math - Reasoning and Strategies” là tài liệu hỗ trợ đắc lực, giúp hệ thống hóa kiến thức, rèn luyện kỹ năng suy luận và nâng cao khả năng giải quyết các dạng toán trong bài thi. Đọc thử tại đây.
SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.
Nguồn tham khảo
“SAT PEMDAS Definition, Rule, and Steps to Use with Examples.” Testbook Edu Solutions, https://testbook.com/en-us/mathematics/pemdas. Accessed 18 August 2025.

Bình luận - Hỏi đáp