Z-score là gì? Cách tính trong thống kê và ứng dụng vào SAT® Math
Key takeaways
Z-score: đo độ lệch so với trung bình bằng số σ
Công thức: z = (x – μ)/σ
Phân tích dạng bài z-score phổ biến
3 bước giải bài tập z-score trong SAT
Trong thống kê, z-score là một công cụ dùng để chuẩn hóa dữ liệu, hỗ trợ so sánh kết quả giữa các nhóm khác nhau và cho thấy một giá trị nằm ở đâu trong phân phối chuẩn. Đối với người học Việt Nam, khái niệm này đôi khi gây khó khăn ban đầu vì ít được đề cập trong chương trình phổ thông, đặc biệt là các nội dung về độ lệch chuẩn hay phân phối chuẩn. Tuy nhiên, khi đã hiểu rõ công thức và cách áp dụng, z-score lại trở thành một phương tiện hữu ích để giải quyết nhiều dạng bài trong SAT.
Bài viết dưới đây sẽ cung cấp cho người học từ định nghĩa, công thức, cách tính z-score đến ứng dụng thực tế trong bài thi SAT math, giúp người học tiếp cận khái niệm này một cách hệ thống và dễ hiểu.
Z-score là gì?
Z-score (còn gọi là standard score) là một chỉ số quen thuộc trong thống kê, được dùng để đo lường khoảng cách giữa một giá trị dữ liệu cá nhân và giá trị trung bình của toàn bộ tập hợp. Khoảng cách này không tính bằng đơn vị gốc (như cm, kg, điểm số), mà tính bằng số đơn vị độ lệch chuẩn – tức là thước đo mức độ phân tán của dữ liệu. Hiểu một cách đơn giản, z-score cho người học biết một quan sát “cách xa” trung bình bao nhiêu lần độ lệch chuẩn.
Nếu z-score > 0, quan sát cao hơn trung bình.
Nếu z-score < 0, giá trị thấp hơn trung bình.
Nếu z-score = 0, dữ liệu đúng bằng trung bình.
Nhờ được chuẩn hóa theo độ lệch chuẩn, z-score loại bỏ hoàn toàn ảnh hưởng của đơn vị đo, giúp việc so sánh dữ liệu từ những nguồn khác nhau trở nên dễ dàng. Ví dụ, người học có thể so sánh điểm toán và điểm văn của một học sinh bằng z-score, thay vì chỉ nhìn vào điểm số thô vốn có thang đo khác nhau.
Tìm hiểu thêm:
Tại sao z-score quan trọng trong phân tích dữ liệu?
Z-score đặc biệt hữu ích vì nó đưa dữ liệu về cùng một thang đo chuẩn, trong đó trung bình bằng 0 và độ lệch chuẩn bằng 1. Điều này giống như “chuẩn hóa mặt bằng” để mọi dữ liệu đều được đo trên cùng một hệ quy chiếu. Nhờ vậy, người học có thể so sánh trực tiếp các giá trị đến từ những tập dữ liệu khác nhau, ngay cả khi chúng vốn sử dụng các đơn vị đo khác nhau (ví dụ: điểm thi, chiều cao, cân nặng).
Không chỉ dừng lại ở việc so sánh, chỉ số z-score còn giúp phát hiện những quan sát bất thường trong dữ liệu. Trong thống kê, một giá trị có |z| lớn, chẳng hạn lớn hơn 3, thường được coi là ngoại lệ (outlier). Điều này cực kỳ quan trọng trong phân tích vì các ngoại lệ có thể báo hiệu sai sót đo lường, hoặc ngược lại, cho thấy một hiện tượng đặc biệt cần chú ý. Ngoài ra, z-score còn gắn liền với việc ước lượng xác suất trong phân phối chuẩn. Các nhà nghiên cứu thường dùng nó để đánh giá mức độ tin cậy, rủi ro hay khả năng xảy ra của một kết quả, từ đó hỗ trợ ra quyết định khoa học và khách quan hơn.
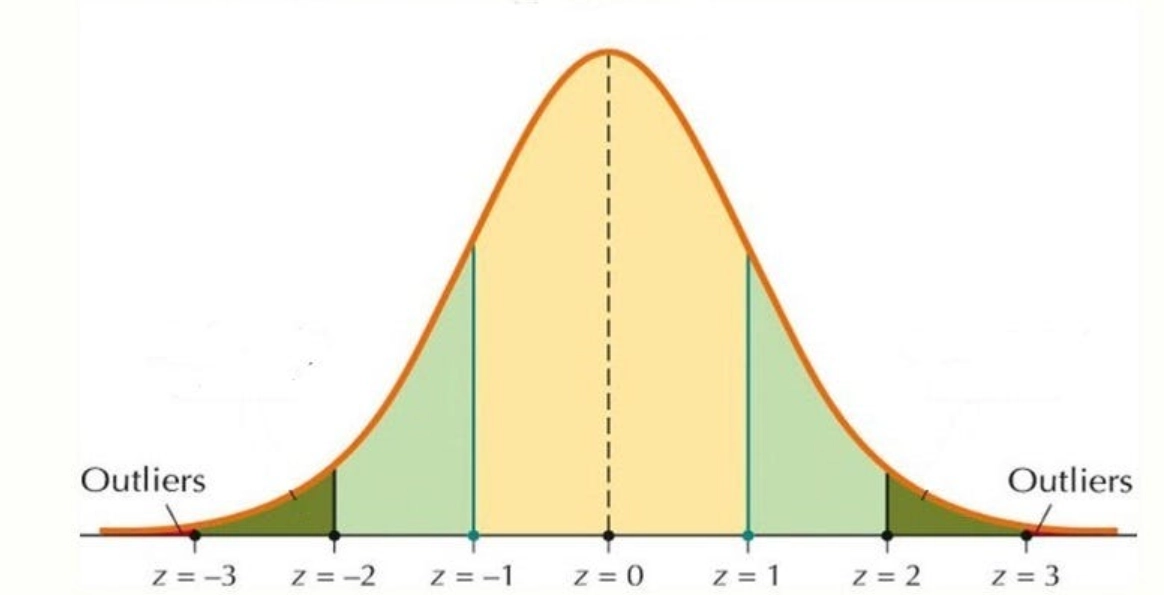
Mối liên hệ giữa z-score với phân phối chuẩn
Phân phối chuẩn (normal distribution) là một trong những phân phối cơ bản nhất của thống kê, có dạng “hình chuông” cân đối quanh giá trị trung bình. Hai đặc trưng quan trọng nhất của nó là: (1) trung bình và (2) độ lệch chuẩn. Khi người học quy đổi dữ liệu sang z-score, toàn bộ phân phối ban đầu được chuyển thành “phân phối chuẩn tắc” (standard normal distribution), có trung bình bằng 0 và độ lệch chuẩn bằng 1.
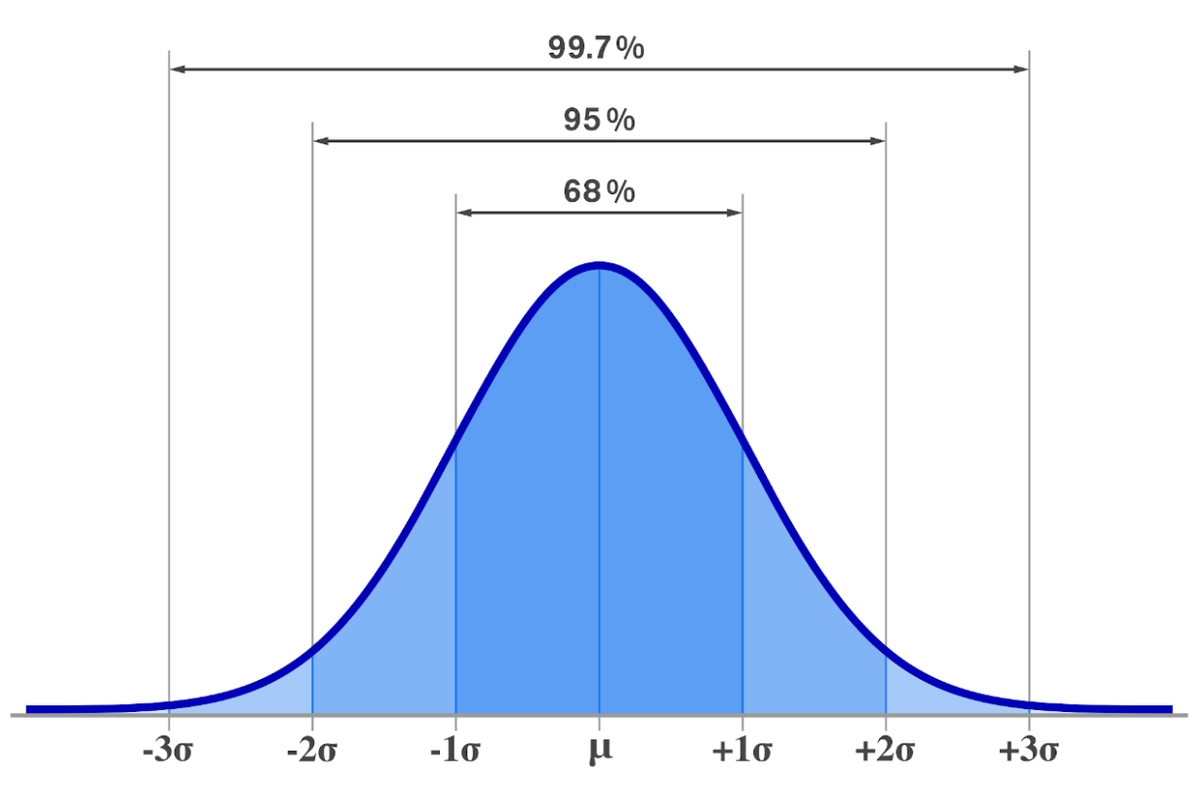
Điều này mang lại lợi ích lớn: ta có thể sử dụng bảng z hoặc phần mềm thống kê để nhanh chóng tìm xác suất một giá trị xuất hiện. Ngoài ra, z-score gắn liền với quy tắc 68–95–99.7:
Khoảng 68% dữ liệu sẽ nằm trong ±1 độ lệch chuẩn quanh trung bình.
Khoảng 95% dữ liệu nằm trong ±2 độ lệch chuẩn.
Khoảng 99.7% dữ liệu nằm trong ±3 độ lệch chuẩn.
Nhờ quy tắc này, z-score trở thành công cụ trực quan để dự đoán, diễn giải và đánh giá dữ liệu, giúp người học hiểu rõ hơn về phân phối xác suất và sự biến động của thông tin trong thực tế.
Công thức tính z-score
Công thức tổng quát
Z-score được tính bằng công thức cơ bản sau:
\(z=\frac{x-\mu}{𝜎}\)
trong đó:
x: là giá trị dữ liệu cụ thể cần đánh giá.
μ (mu): trung bình của toàn bộ tập hợp hoặc quần thể.
σ (sigma): độ lệch chuẩn, thể hiện mức độ phân tán của dữ liệu quanh trung bình.
Đây là công thức chuẩn hóa trực tiếp và được sử dụng rộng rãi nhất trong thống kê. Nhờ công thức này, mọi giá trị trong tập dữ liệu – dù khác nhau về đơn vị đo (cm, kg, điểm số, doanh thu…) – đều có thể được quy đổi về cùng một thang đo chuẩn. Kết quả là người học có thể dễ dàng so sánh các giá trị, kể cả khi xuất phát từ những nguồn dữ liệu hoàn toàn khác nhau.
Chức năng của từng thành phần
x chính là điểm dữ liệu muốn phân tích. Nó có thể là điểm thi của một học sinh trong một kỳ kiểm tra, chiều cao của một người so với nhóm dân số, hoặc doanh thu một ngày của cửa hàng so với doanh thu trung bình.
μ đóng vai trò “mốc chuẩn” để đo xem giá trị x lệch bao nhiêu so với mức trung bình. Không có μ, ta sẽ không biết liệu dữ liệu đang cao hay thấp hơn mặt bằng chung.
σ cho biết dữ liệu phân tán rộng hay hẹp quanh trung bình. Khi σ lớn, dữ liệu trải rộng và dao động nhiều; khi σ nhỏ, dữ liệu tập trung sát quanh trung bình. Nhờ có σ, khoảng cách giữa x và μ được quy đổi thành số “lần độ lệch chuẩn” – đó chính là bản chất của z-score.
Các trường hợp giá trị z-score
Z > 0: dữ liệu cao hơn trung bình, nằm về phía bên phải của đồ thị phân phối. Ví dụ, nếu z = +2, nghĩa là giá trị này cao hơn trung bình đúng 2 độ lệch chuẩn, thường nằm trong nhóm nổi bật.
Z < 0: dữ liệu thấp hơn trung bình, nằm bên trái của phân phối. Ví dụ z = -1.5 cho thấy dữ liệu thấp hơn trung bình 1.5 độ lệch chuẩn, tức nằm ở phía dưới trung bình đáng kể.
Z = 0: dữ liệu đúng bằng trung bình, tức hoàn toàn không lệch sang bên nào cả. Đây là vị trí “chuẩn” trên phân phối chuẩn.
Nhờ cách diễn giải này, z-score không chỉ cho biết dữ liệu cao hay thấp, mà còn định lượng rõ ràng “cao hơn bao nhiêu” hoặc “thấp hơn bao nhiêu” so với trung bình.
Ảnh hưởng của z-score
Việc tính z-score mang lại nhiều lợi ích quan trọng:
So sánh dữ liệu: vì đã chuẩn hóa về cùng thang đo, người học có thể so sánh trực tiếp giữa nhiều tập dữ liệu khác nhau. Ví dụ, so sánh điểm Toán (thang 10) và điểm SAT (thang 1600) bằng cách đưa về z-score.
Phát hiện ngoại lệ (outliers): những điểm dữ liệu có |z| quá lớn, thường lớn hơn 3, được coi là ngoại lệ vì nằm rất xa trung bình. Đây là thông tin cực kỳ quan trọng trong nghiên cứu và phân tích dữ liệu.
Tính xác suất trong phân phối chuẩn: thông qua bảng Z (Z-table), người học có thể nhanh chóng ước lượng xác suất một giá trị xuất hiện, từ đó phục vụ kiểm định giả thuyết hoặc ra quyết định dựa trên độ tin cậy thống kê.
Ứng dụng đa lĩnh vực: z-score được sử dụng rộng rãi trong nhiều ngành, từ khoa học xã hội, kinh tế, tài chính, giáo dục cho đến khoa học dữ liệu và trí tuệ nhân tạo. Ví dụ, nhà phân tích tài chính dùng z-score để đánh giá rủi ro cổ phiếu, còn nhà nghiên cứu giáo dục dùng để so sánh thành tích học tập của học sinh giữa các kỳ thi khác nhau.
Đọc thêm: SAT Percentile là gì? Cách tính điểm phần trăm SAT (2025)
Hướng dẫn tính z-score từng bước
Bước 1: Xác định giá trị trung bình (μ).
Giá trị trung bình là nền tảng để so sánh và chuẩn hóa dữ liệu. Để tính giá trị trung bình, người học cộng tất cả các giá trị trong tập dữ liệu rồi chia cho số lượng phần tử. Ví dụ, với dãy số 5, 6, 7, 8, 9 thì trung bình bằng (5 + 6 + 7 + 8 + 9) / 5 = 7.
Bước 2: Tìm độ lệch chuẩn (σ).
Độ lệch chuẩn cho biết dữ liệu tập trung gần hay phân tán xa so với trung bình. Trước hết, lấy từng giá trị trừ đi trung bình, bình phương hiệu số này, cộng tất cả lại, chia cho số lượng phần tử, rồi lấy căn bậc hai. Độ lệch chuẩn được tính như sau:
\(\sigma=\sqrt{\frac{\Sigma\left(x-\mu\right)^2}{n}}\)
Nếu σ nhỏ, dữ liệu phân bố sát với trung bình; nếu σ lớn, dữ liệu trải rộng và có nhiều biến động hơn.
Bước 3: Áp dụng công thức và tính toán.
Sau khi đã có μ và σ, người học có thể dễ dàng tính được z-score dựa vào công thức:
\(z=\frac{x-\mu}{𝜎}\)
Ứng dụng z-score trong bài thi SAT Math
Dạng bài phổ biến nhất liên quan đến z-score trong bài thi SAT Math là dạng bài đưa ra hai hoặc nhiều biểu đồ (dot plot, histogram hoặc box plot) thể hiện các phân bố dữ liệu khác nhau và yêu cầu người học xác định tập dữ liệu nào có độ lệch chuẩn lớn hơn hoặc nhỏ hơn. Mục tiêu của dạng này là đánh giá khả năng nhận biết mức độ phân tán của dữ liệu quanh giá trị trung bình (mean). Dữ liệu càng tập trung gần trung tâm thì độ lệch chuẩn càng nhỏ, còn dữ liệu càng trải rộng hoặc có nhiều giá trị ở hai đầu thì độ lệch chuẩn càng lớn.
Chiến lược giải bài tập z-score trong SAT:
Bước 1: Quan sát dạng biểu đồ. Xác định xem đề cho biểu đồ cột, biểu đồ chấm hay biểu đồ hộp. Kiểm tra kỹ xem các biểu đồ có cùng thang đo trên trục giá trị hay không, vì chỉ khi cùng thang đo mới có thể so sánh độ lệch chuẩn một cách chính xác.
Bước 2: Nhận diện mức độ tập trung và phân tán của dữ liệu. Nếu biểu đồ có các giá trị tập trung nhiều ở khu vực trung tâm (biểu đồ cao và hẹp ở giữa) thì dữ liệu ít dao động, nghĩa là độ lệch chuẩn nhỏ. Ngược lại, nếu các giá trị trải rộng, xuất hiện nhiều ở hai đầu hoặc phân bố phẳng hơn, thì dữ liệu dao động mạnh hơn và có độ lệch chuẩn lớn.
Bước 3: Đưa ra kết luận theo yêu cầu của đề. So sánh mức độ phân tán của các tập dữ liệu và kết luận xem tập nào có độ lệch chuẩn lớn hơn hoặc nhỏ hơn.
Xem thêm:
Cách làm dạng bài Problem Solving and Data Analysis trong SAT Math
Cách làm dạng bài Probability and Relative frequency và bài tập
Bài tập thực hành
Bài 1: Which of the following statements must be true?
I. The median of data set C is equal to the median of data set D.
II. The standard deviation of data set C is equal to the standard deviation of data set D.
A) I only
B) II only
C) I and II
D) Neither I nor II
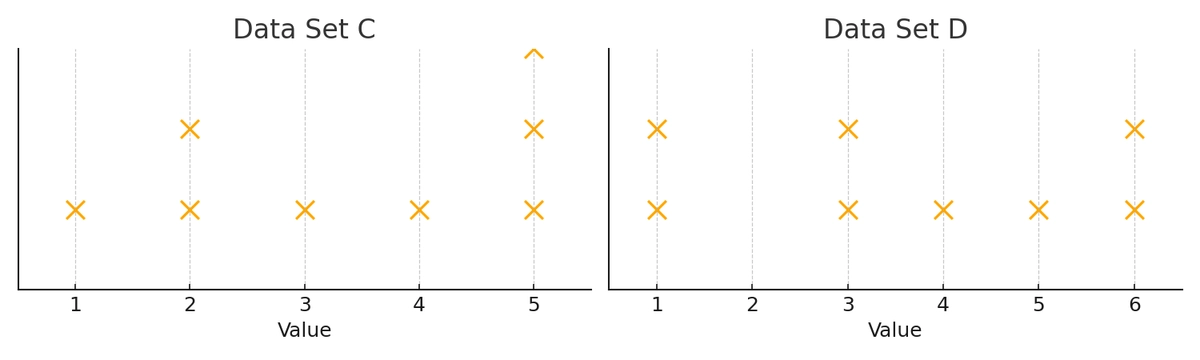
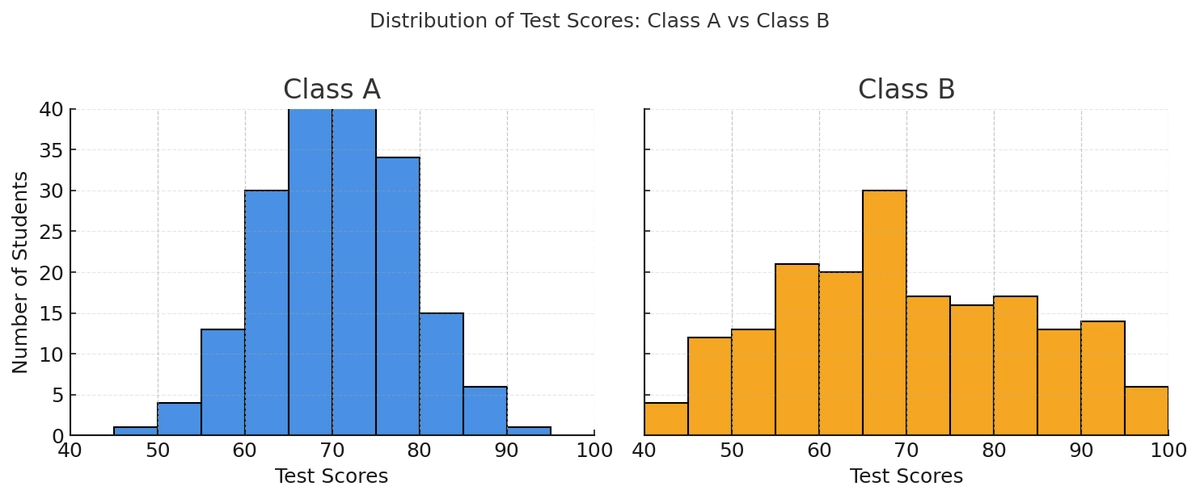
Bài 2: Which of the following statements is true based on the histograms?
A) The standard deviation of Class A’s scores is greater than that of Class B’s.
B) The standard deviation of Class A’s scores is less than that of Class B’s.
C) The two classes have approximately the same standard deviation.
D) It is not possible to determine which class has a larger standard deviation.
Đáp án
Bài 1: A
Bài 2: B
Tổng kết
Bài viết trên đã cung cấp cho người học từ định nghĩa, công thức, cách tính đến ứng dụng thực tế của z-score trong bài thi SAT math, giúp người học tiếp cận khái niệm này một cách hệ thống và dễ hiểu. Việc nắm vững công thức cũng như ý nghĩa của z-score không chỉ giúp làm bài nhanh chóng mà còn rèn luyện tư duy phân tích dữ liệu. Để đạt kết quả cao, người học nên thường xuyên luyện tập: bắt đầu với các bài tính z-score cơ bản rồi nâng dần độ khó bằng bài so sánh. Càng thực hành nhiều, người học sẽ càng tự tin và chính xác khi gặp dạng toán này trong SAT Math.
Ngoài ra, để nâng cao kỹ năng làm toán trong bài thi SAT nói riêng và kỹ năng làm bài thi SAT cả hai phần thi Math và Reading and Writing, người học có thể tham khảo các khóa học SAT tại ZIM Academy.
SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.

Bình luận - Hỏi đáp