Circle equations - Công thức, chiến lược làm bài và bài tập

Đây là một dạng toán nằm trong SAT Math - Geometry and Trigonometry (Hình học và các biểu thức hình học), một dạng toán khá quen thuộc nằm trong chương trình Toán học THPT dành cho học sinh Việt Nam. Bài viết sẽ giới thiệu đến người đọc cụ thể về Circle Equations (Phương trình đường tròn), và các bài tập vận dụng dạng toán này.

Tổng quát về Circle Equations (Phương trình đường tròn)

Bài toán về Circle Equations (Phương trình đường tròn) là một trong những dạng bài quen thuộc nằm trong phần SAT Math Geometry and Trigonometry. 

Xét trên hệ trục tọa độ Oxy, đường tròn (C) có tâm đường tròn I (a;b) và độ dài bán kính r, được viết dưới dạng phương trình sau:

\[(x-a)^{2^{}}+(y-b)^2=r^2\] Khi diễn giải phương trình một cách đầy đủ, ta có:

\[x^{^2}+y^{^2}-2ax-2by+C=0\] Đối với phương trình đầy đủ:

• a là tọa độ của tâm I trên Ox

• b là tọa độ của tâm I trên Oy

• C=

  a² + b² - r²

  và C là một hằng số

Phương trình trên được coi là phương trình của đường tròn (C) khi \[\sqrt{a^{^2}+b^{^2}-C}\]

với  a² + b² - C > 0

Một số công thức bổ trợ

Công thức tính khoảng cách giữa 2 điểm A(x1;y1) và B(x2;y2)
\[AB=\sqrt{\left(x2-x1\right)^{2^{}}+\left(y2-y1\right)^2}\]

Công thức tìm trung điểm của đoạn thẳng dựng bới A(x1;y1) và B(x2;y2):

• Tọa độ trung điểm của điểm I được xác định như sau:

x = (x1+x2)/2

y = (y1+y2)/2

Vậy tọa độ trung điểm I((x1+x2)/2; (y1+y2)/2)

Đọc thêm: Unit circle trigonometry - Chiến lược làm bài và bài tập

Chiến lược làm dạng bài Circle Equations trong SAT Math

Xác định vị trí của đường tròn trên mặt phẳng Oxy hoặc các đại lượng của đường tròn khi cho trước phương trình

Dựa trên các đại lượng cơ bản của đường tròn như tâm và bán kính, hoặc từ một phương trình cho trước, đề bài sẽ yêu cầu người học xác định xem đường tròn được vẽ như thế nào trên mặt phẳng tọa độ Oxy.

Để xác định vị trí, ta cần nhìn vào phương trình đường tròn được cho trước:

Đối với dạng tổng quát:

Từ phương trình tổng quát, ta sẽ tìm được tọa độ tâm là I(a;b)

• \[(x-a)^2+(y-b)^2=D=r^2\]

  Từ phương trình đường tròn tiêu chuẩn, ta sẽ xác định được bán kính bằng cách lấy căn bậc hai của D ( hằng số của vế bên phải)

• Sau đó, dựng lại đường tròn trên mặt phẳng Oxy theo thứ tự, lấy tọa độ tâm, xác định góc phần tư mà đường tròn nằm trên.

Đối với dạng đầy đủ:

• \[x^{^2}+y^{^2}-2ax-2by+C=0\]
  Từ biểu thức đầy đủ trên, xác định được I(a;b), sau đó xác định r=\[\sqrt{a^{^2}+b^{^2}-C}\]

• Các bước tiếp theo tương tự như dạng phương trình tổng quát.

Ví dụ 1: (x+2)² + (y-1)² = 9

The given circle equation describes a specific geometric shape. Which of the following options correctly represents this shape?

Look at the given equation:

(x+2)² + (y-1)² = 9

We can see that the center of the circle is I(-2,1) and the radius is 3. We can conclude that the circle is in quarter II of the graph.

With r=3, the circle goes through point (-2, 4). Therefore, the graph explains the equation is option 1.

Dịch nghĩa:

Nhìn vào phương trình đề bài cho trước

Ta xác định được đường tròn có tâm I(-2,1) và bán kính là 3. Chúng ta có thể kết luận rằng đường tròn nằm trong góc phần tư thứ 2 (góc trái trên) của đồ thị.

Với r=3, đường tròn đi qua điểm (-2;4). Chính vì thế, đồ thị miêu tả đúng với phương trình là đáp án 1.

Ví dụ 2: Given the equation of a circle x²+ y²-6x+8y=0, determine the center and radius of the circle.

Based on the model equation:

\[x^2+y^2-2ax-2by+C=0\]

We can determine that 2a = 6, 2b = - 8, C = 0. 

So a = 3, b = -4, C= 0. Using the function of finding the radius, we have:

x² + y² - 6x + 8y = 25

So the given circle equation defines a circle with the center (3;-4), and the radius r = 5

Dịch nghĩa

Dựa vào phương trình đầy đủ cho trước, ta xác định được 2a = 6, 2b = - 8, C = 0. 

Thay a = 3, b = -4, C= 0 vào biểu thức tìm r cho trước, ta được

x² + y² - 6x + 8y = 25

Vậy phương trình đường tròn cho trước biểu diễn đường tròn có tâm (3;-4) và bán kính r = 5.

Xác định phương trình đường tròn dựa trên các đại lượng cho trước

Để xác định phương trình đường tròn dựa trên đại lượng cho trước, ta cần dựa vào phương trình đường tròn tiêu chuẩn, theo các bước sau

• Xác định tâm của đường tròn

• Xác định độ dài bán kính của đường tròn

• Thay các đại lượng tìm được vào phương trình đường tròn 

Ví dụ 1:

A circle in the (xy)-plane has a center at (1/2, -3/4) and a diameter of 5/8. What is the equation of the circle?

The radius of the circle is r = d/2 = 5/16

Place the center and the radius in the standard equation, the equation of the circle is

x² + y² - x + y. (3/2) = 25/256

Dịch nghĩa
Ta có bán kính đường tròn là: 

r = d/2 .⅝= 5/16

Thay các giá trị tìm được vào phương trình tiêu chuẩn, phương trình của đường tròn là:
(x-1/2)² + (y+3/4)² = 25/256

Ví dụ 2: A circle in the (xy)-plane has a center at (2, -1) and passes through the point (5, 3). What is the equation of the circle?

Because the circle goes through the point (5,3), we use the distance formula to find the radius:

\[r=\sqrt{\left(x2-x1\right)^{2^{}}+\left(y2-y1\right)^2}=\sqrt{(5-2)^2+(3-(-1))^2}=\sqrt{3^2+4^2}=5\]

So the circle has a center of (2;-1) and a radius of 5

The equation of the circle is

(x - 2)² + (y+1)² = 25

Dịch nghĩa

Vì đường tròn đi qua điểm (5;3), ta sử dụng công thức tính khoảng cách từ tâm đến điểm đó để tìm độ dài bán kính:

r = sqrt((x2-x1)² + (y2-y1)²= sqrt((5-2)² + (3-(-1))²) = sqrt( 3² + 4²) = 5

Vậy đường tròn có tâm là ( -2;1) và độ dài bán kính là 5

Phương trình đường tròn là:

(x - 2)² + (y+1)² = 25

Xác định điểm nằm hoặc không nằm trên đường tròn

Bằng cách thay các tọa độ điểm vào phương trình đường tròn cho trước, nếu phương trình cho ra kết quả của 2 vế bằng nhau, ta kết luận phương trình đó nằm trên đường tròn.

Ví dụ:

The equation of this circle is

(x - 2)² + ( y − 9)² =  25

Which of the following points does the circle go through?

1. M(2;14)

2. N(3;7)

3. P(0;6)

4. Q(5;9)

To determine which point lies on the given circle, we have to check if the point satisfies the equation:

• Point M(2, 14): (2 - 2)²+ (14 - 9)² = 0 + 25 = 25

• Point N(3, 7): (3 - 2)² + (7 - 9)² = 1 + 4 = 5 ≠ 25

• Point P(0, 6): (0 - 2)² + (6 - 9)² = 4 + 9 = 13 ≠ 25

• Point Q(5, 9): (5 - 2)² + (9 - 9)² = 9 + 0 = 9 ≠ 25

So, the circle goes through point M(2, 14).

Dịch nghĩa:

Để xác định điểm nào nằm trên đường tròn được cho bởi phương trình

chúng ta cần kiểm tra xem mỗi điểm có thỏa mãn phương trình hay không.

• Point M(2, 14): (2 - 2)²+ (14 - 9)² = 0 + 25 = 25

• Point N(3, 7): (3 - 2)² + (7 - 9)² = 1 + 4 = 5 ≠ 25

• Point P(0, 6): (0 - 2)² + (6 - 9)² = 4 + 9 = 13 ≠ 25

• Point Q(5, 9): (5 - 2)² + (9 - 9)² = 9 + 0 = 9 ≠ 25

Vậy đường tròn đi qua điểm M(2;14)

Một số lưu ý về dạng toán Circle Equations

• Hệ số của x² và y² luôn phải bằng nhau: Vì phương trình đường tròn chỉ tồn tại dưới dạng

  x² + y² -2ax -2by + C= 0, nên hệ số phải bằng nhau để phương trình có thể rút gọn về dạng cơ bản

• Để ý rõ đại lượng đề bài đề cập đến: Người học lưu ý rõ hai đại lượng bán kính và đường kính, tránh sai sót trong quá trình làm bài. Nếu bài đề cập đến đường kính, người học cần chia đôi để tìm bán kính.

Bài tập vận dụng

Ex 1:  A circle in the (xy)-plane has a diameter with endpoints (1, -3) and (1, 7). An equation of this circle is (x - 1)2 + (y - 2)² = r² where (r) is a positive constant. What is the value of (r)?

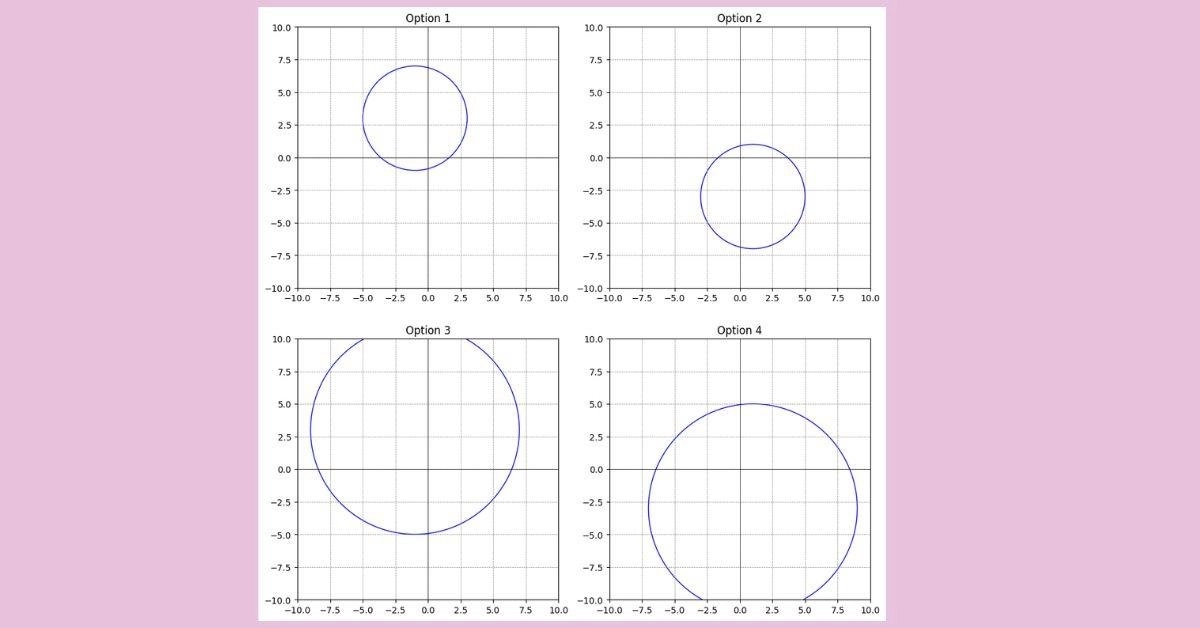
Ex 2: Consider the equation

Which of the following is a graph of the given equation?

(x-1)² + (y+3)² = 16.

Ex 3: The graph of the below equation in the xy-plane is a circle.

x² + 4x + y² - 6y = 23

What is the length of the circle’s radius?

Ex 4:

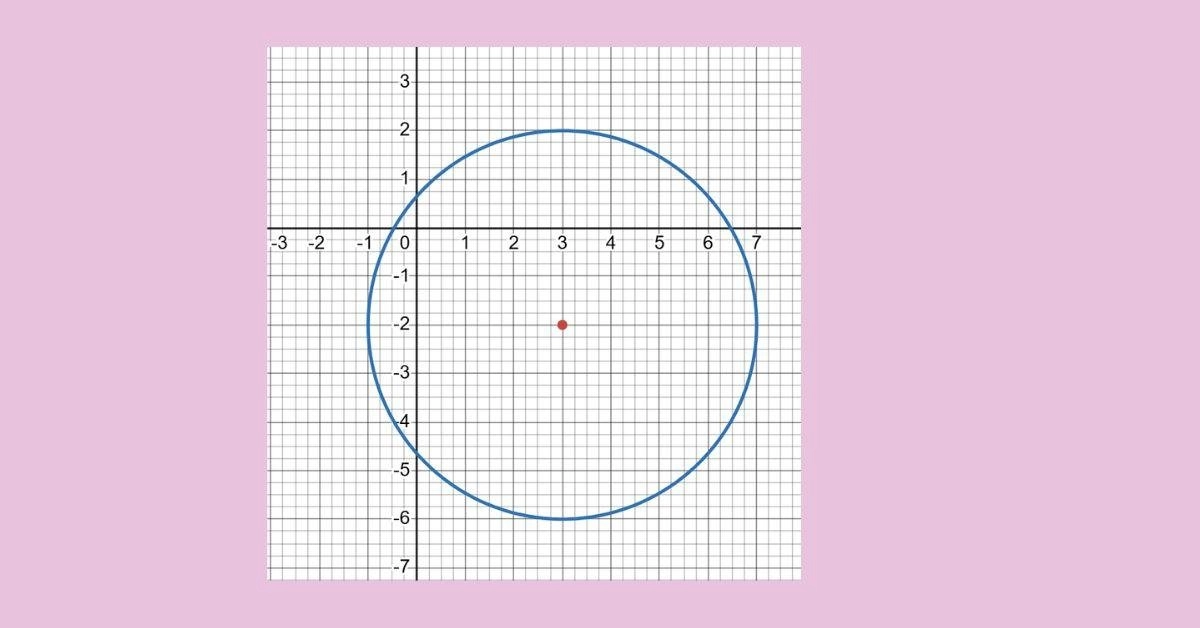
Which of the following circle equations represents the graph?
A. (x+3)² + (y-2)²= 4

B. (x-3)² + (y+2)²= 16

C.(x+3)² + (y-2)²= 16

D.(x-3)² + (y-2)²= 16

Ex 5: An equation of a circle is (x + 1)² + (y - 4)² = 36

Which of the following points does the circle go through?

A. (-1, 9)

B. (2, 4)

C. (-4, 4)

D. (-1, -2)

Ex 6: A circle in the (xy)-plane has a center at (-4, 2) and passes through the point (0, 6). What is the equation of the circle?

Ex 7: A circle in the (xy)-plane has a center at (3/4, -1/2) and a diameter of 3/5. What is the equation of the circle?

Ex 8: A circle in the (xy)-plane has a diameter with endpoints (3, -2) and (3, 8). Find the equation of the circle.

Đáp án

Ex 1: r = 5

Ex 2: Option 2

Ex 3: r = 6

Ex 4: B .

(x-3)² + (y+2)²= 16

Ex 5: D. (-1; -2)

Ex 6: (x+4)² + (y-2)²= 32

Ex 7: (x-3/4)² + (y+ 1/2)²= 9/100

Ex 8: (x-3)² + (y-3)²= 25

Gợi ý: Áp dụng công thức tính khoảng cách

Người học có thể tham khảo thêm:

• SAT Math Question: Hình học và lượng giác (góc, tam giác & hình tròn)

• SAT Math formulas - Tổng hợp các công thức thường gặp trong SAT Math

Tổng kết

Bài viết đã giúp người học hiểu rõ về các khái niệm liên quan đến Circle equations và một số dạng bài Circle equations phổ biến trong SAT Math. Nếu người học gặp nhiều khó khăn trong quá trình tự học SAT, có thể đến với chuyên mục tự học SAT của ZIM Academy để biết thêm nhiều kiến thức hữu ích.

Ngoài ra, để giúp thí sinh giải quyết các dạng toán hiệu quả trong bài thi SAT Math, đội ngũ chuyên môn tại ZIM đã biên soạn tựa sách Think in SAT Digital Math - Reasoning and Strategies. Với mỗi dạng bài, cuốn sách sẽ cung cấp kiến thức cơ bản, các ví dụ và cách giải mẫu, cuối cùng là bài tập luyện tập kèm đáp án có giải thích chi tiết. Đọc thử tại đây.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.