Compound interest - Bài toán lãi kép & chiến lược làm bài hiệu quả

SAT (Scholastic Assessment Test) là bài thi chuẩn hoá nhằm đánh giá năng lực của học sinh được phát triển và sở hữu bởi College Board - tổ chức giáo dục phi lợi nhuận tại Mỹ. Kỳ thi SAT thường được tổ chức vào các tháng 3, 5, 6, 10, 11 và 12. Từ tháng 3 năm 2023, bài thi SAT chính thức được chuyển sang hình thức thi trên máy, gọi là Digital SAT.

Compound Interest (lãi kép) là một trong những dạng toán quan trọng thường xuất hiện trong phần Advanced Math của bài thi SAT Digital Math. Dạng toán về lãi kép không chỉ kiểm tra khả năng vận dụng công thức lãi suất mà còn yêu cầu thí sinh hiểu sâu về bản chất của hàm mũ - một nội dung quan trọng trong đại số. Bài viết này của Anh ngữ ZIM sẽ giúp người học nắm vững dạng toán Compound Interest, tránh những lỗi sai thường gặp và áp dụng chiến lược giải nhanh để đạt điểm tối đa phần SAT Math.

Tổng quan về Compound Interest

Compound Interest (lãi kép) là một dạng toán quen thuộc và đặc biệt quan trọng trong phần Advanced Math của bài thi SAT Digital Math. Đây là nội dung kiểm tra khả năng vận dụng kiến thức đại số vào những tình huống tài chính thực tiễn, cụ thể là các bài toán về tăng trưởng giá trị của một khoản đầu tư hoặc khoản tiền gửi theo thời gian. Các bài toán về lãi kép thường được đưa vào nhằm kiểm tra khả năng hiểu và áp dụng các hàm số mũ – một nội dung cốt lõi trong đại số bậc phổ thông.

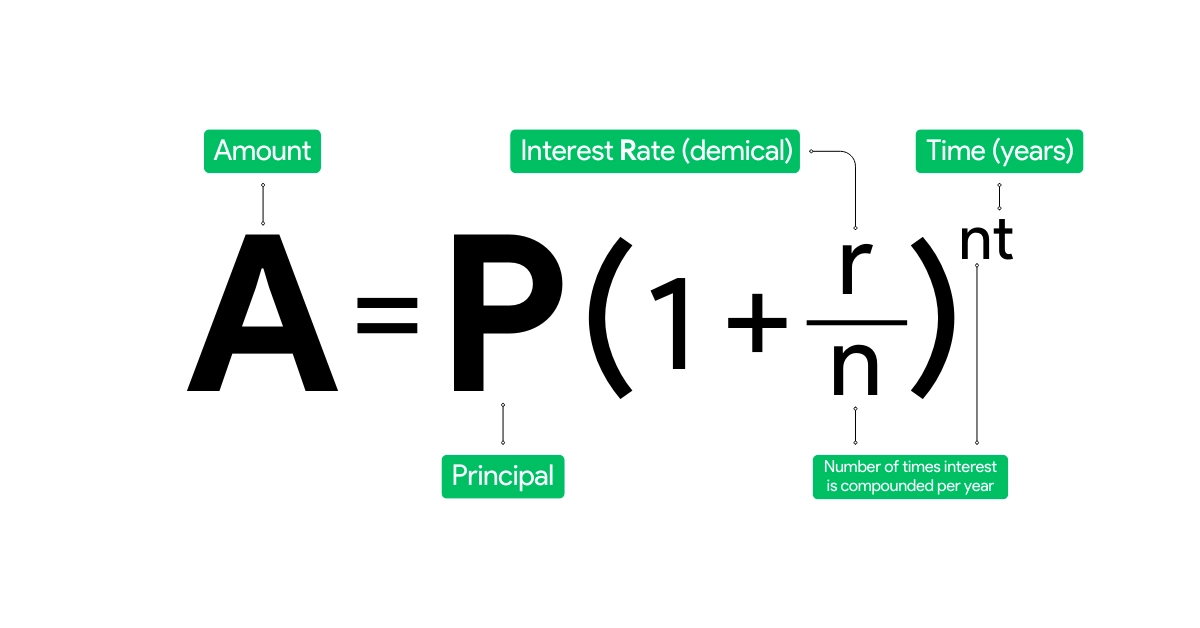
Về mặt bản chất, lãi kép là khái niệm chỉ việc số tiền lãi không chỉ được tính trên số vốn gốc ban đầu mà còn trên cả phần lãi đã phát sinh từ các kỳ trước đó. Điều này làm cho tổng số tiền nhận được sau mỗi kỳ tăng trưởng nhanh hơn so với lãi đơn, do lãi được “cộng dồn” theo thời gian. Công thức dùng để tính lãi kép là:

\(A=P\times\left(1+\frac{r}{n}\right)^{nt}\)

Trong đó:

• A là số tiền tích lũy sau t năm.

• P là số tiền gốc ban đầu.

• r là lãi suất hàng năm dưới dạng thập phân.

• n là số lần tính lãi trong một năm.

• t là tổng số năm gửi tiền.

Chẳng hạn, nếu một học sinh đầu tư 10,000 đô la vào một tài khoản tiết kiệm với lãi suất 8% mỗi năm và lãi được tính theo quý, học sinh đó có thể áp dụng công thức trên để xác định chính xác số tiền nhận được sau một khoảng thời gian nhất định.

Dạng bài toán lãi kép giúp người học hiểu các khái niệm như lãi suất ngân hàng, lãi suất đầu tư hay các khoản vay là những tình huống phổ biến mà người học sẽ gặp phải sau này khi đi học hoặc đi làm. Bên cạnh đó, dạng toán này yêu cầu người học vận dụng các hàm số mũ trong bối cảnh cụ thể – điều này giúp kiểm tra sâu hơn năng lực giải quyết vấn đề của người học chứ không chỉ dừng lại ở thao tác giải phương trình thuần túy.

Việc hiểu và vận dụng tốt dạng toán này không chỉ giúp học sinh đạt điểm cao trong phần SAT Math mà còn giúp trang bị kiến thức thiết thực về quản lý tài chính cá nhân trong tương lai.

Xem thêm: SAT Math formulas - Tổng hợp các công thức thường gặp trong SAT Math

Chiến lược làm dạng toán Compound Interest trong SAT Math

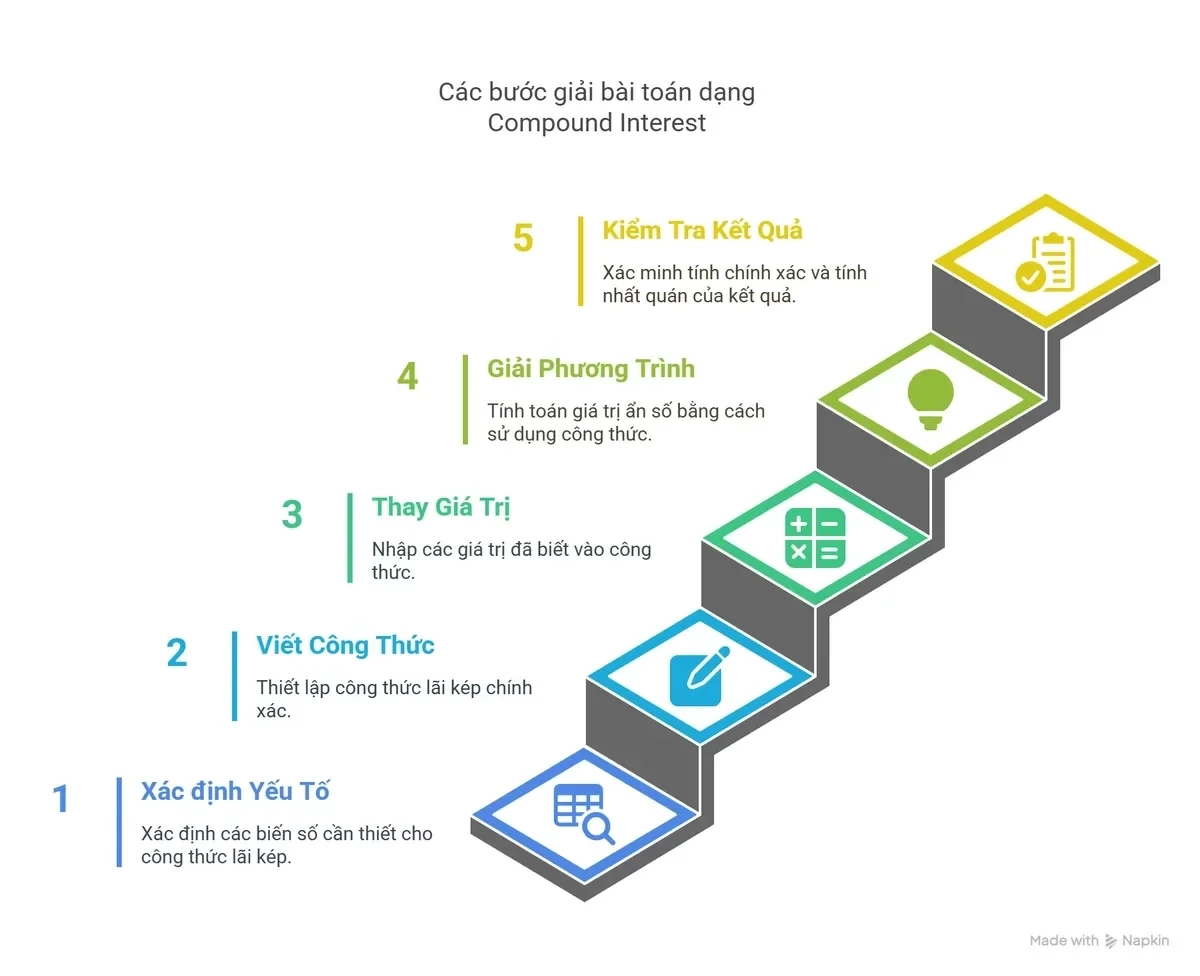
Các bước giải bài toán dạng Compound Interest:

Bước 1: Xác định các yếu tố trong công thức: Principal (P), Annual Interest Rate (r), Number of Compounding Periods per Year (n), Time in Years (t), và Final Amount (A).

Bước 2: Viết đúng công thức lãi kép:

\(A=P\times\left(1+\frac{r}{n}\right)^{nt}\)

Bước 3: Thay các giá trị đã cho vào công thức.

Bước 4: Giải phương trình để tìm ẩn số còn thiếu (A, P, t, hoặc r).

Bước 5: Kiểm tra lại kết quả và đảm bảo rằng các đơn vị (percent → decimal, thời gian → years, tần suất cộng lãi → lần/năm) đã được chuyển đổi đúng.

Ví dụ: A sum of $2,000 is invested at an annual interest rate of 4%, compounded quarterly. What will the total amount be in the account after 3 years? (Một khoản tiền $2,000 được đầu tư với lãi suất hàng năm là 4%, tính lãi kép theo quý. Tổng số tiền trong tài khoản sau 3 năm sẽ là bao nhiêu?)

(A) $2,240.00
(B) $2,250.88
(C) $2,253.65
(D) $2,256.48

Step 1: Identify variables:
P = 2000 (principal)
r = 0.04 (4% annual interest rate in decimal form)
n = 4 (quarterly compounding)
t = 3 (years)

Step 2: Write the compound interest formula:

\(A=P\times\left(1+\frac{r}{n}\right)^{nt}\)

Step 3: Substitute known values into the formula:

\(A=2000\times\left(1+\frac{0.04}{4}\right)^{4\times3}\)
\(A=2000\times\left(1+0.01\right)^{12}\)

\(A=2000\times\left(1.01\right)^{12}\)

Step 4: Calculate:

A = 2000 × 1.126825 ≈ 2253.65

Closest answer: (C) $2,253.65.

Step 5: Double-check all variables and units – correct.

(dịch)

Bước 1: Xác định các đại lượng:
P = $2,000 (số tiền gốc)
r = 0.04 (lãi suất hằng năm, chuyển về dạng thập phân)
n = 4 (lãi cộng theo quý)
t = 3 (năm)

Bước 2: Viết công thức lãi kép:

\(A=P\times\left(1+\frac{r}{n}\right)^{nt}\)

Bước 3: Thay giá trị vào công thức:

\(A=2000\times\left(1+\frac{0.04}{4}\right)^{4\times3}\)
\(A=2000\times\left(1+0.01\right)^{12}\)

\(A=2000\times\left(1.01\right)^{12}\)

Bước 4: Bấm máy tính:

A = 2000 × 1.126825 ≈ 2253.65

Phương án đúng nhất là (C) $2,253.65.

Bước 5: Kiểm tra lại đơn vị và số liệu – đúng.

Tìm hiểu thêm: Quadratic and exponential word problems Hướng dẫn làm bài và bài tập

Một số lưu ý

Khi giải các bài toán về Compound Interest trong SAT Math, người học cần chú ý một số điểm quan trọng để tránh những sai lầm thường gặp gây mất điểm đáng tiếc. Trước hết, điều quan trọng nhất là phải đọc kỹ đề bài để xác định đúng tần suất tính lãi (n). Trong nhiều trường hợp, đề bài sử dụng các cụm từ như “compounded annually”, “compounded quarterly” hoặc “compounded monthly” để chỉ số lần tính lãi trong năm, tương ứng lần lượt với n = 1, n = 4 và n = 12. Việc nhầm lẫn giá trị của n sẽ dẫn đến sai toàn bộ kết quả. Bên cạnh đó, lãi suất hàng năm (Annual Interest Rate) luôn được cho dưới dạng phần trăm, nên người học phải chuyển đổi về số thập phân bằng cách chia cho 100 trước khi thay vào công thức. Ví dụ, lãi suất 5% phải được đổi thành 0.05; nếu quên bước này, kết quả tính toán sẽ chênh lệch rất lớn.

Một sai lầm phổ biến khác là xác định sai khoảng thời gian đầu tư (t). Đề bài thường cho thời gian dưới nhiều dạng khác nhau: năm, tháng hoặc quý. Nếu đề cho số tháng mà lãi được cộng hàng năm thì cần đổi tháng sang năm (bằng cách chia cho 12) trước khi thay vào công thức. Ngoài ra, SAT Digital cho phép sử dụng máy tính, do đó người học nên tận dụng chức năng lũy thừa của máy tính để tránh tính nhẩm sai khi xử lý các số mũ lớn. Cuối cùng, cần nhớ rằng SAT hiếm khi yêu cầu giải phương trình logarit để tìm t hoặc r, trừ khi đáp án ở dạng biểu thức; khi gặp trường hợp này, người học chỉ cần thiết lập đúng công thức là đủ để chọn phương án đúng.

Bài tập ứng dụng

Bài 1: A savings account is opened with $3,000 and earns an annual interest rate of 3%, compounded monthly. What is the total amount in the account after 2 years?

(A) $3,183
(B) $3,200
(C) $3,187
(D) $3,250

Bài 2: A savings account is opened with $6,000 for a four-year period at an annual interest rate of 4% compounded once annually. What is closest to the positive difference between the interest earned in the fourth year and the interest earned in the third year?

(A) $9.60
(B) $10.00
(C) $249.60
(D) $240.00

Đáp án: 1-C / 2-B

Luyện tập thêm: Bài tập lũy thừa (Exponents) trong SAT Math kèm đáp án và giải thích

Tổng kết

Bài viết trên của Anh Ngữ ZIM đã cung cấp cho người học chiến lược làm dạng bài tập lãi kép (compound interest) của bài thi SAT. Bên cạnh đó, để chuẩn bị tốt nhất cho bài thi SAT, người học có thể tham khảo Khóa học SAT của Anh ngữ ZIM.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.