Những điều cần biết về phần Toán Định Lượng trong GMAT và các thuật ngữ Toán Hình Học

Bố cục phần thi Quantitative Section GMAT

Quantitative Section GMAT là phần thi nhằm đánh giá tư duy phân tích của thí sinh dựa trên các khái niệm toán học cơ bản về 3 chủ đề chính là Số học, Đại số và Hình học.

Bài thi yêu cầu thí sinh hoàn thành 31 câu hỏi trắc nghiệm (5 đáp án/câu) trong vòng 62 phút và thí sinh không được sử dụng máy tính bỏ túi trong suốt quá trình làm bài.

Có 2 dạng câu hỏi ở phần này, bao gồm Giải quyết vấn đề (Problem Solving), 18 – 20 câu, và Đánh giá dữ liệu (Data Sufficiency), 11 – 13 câu.

Xem thêm: Giới thiệu về bài thi GMAT

Phân bổ nội dung trong bài Quantitative Section GMAT

Về nội dung, Quantitative Section GMAT bao gồm các câu hỏi dựa trên các khái niệm toán học cơ bản sau:

Những chủ đề thường gặp

Các vấn đề về từ ngữ (Word Problems)

Ở dạng này, những câu hỏi sẽ là các vấn đề thực tế trong cuộc sống, đòi hỏi thí sinh hiểu và giải quyết những vấn đề đó bằng các phương pháp toán học.

Ví dụ. 

“Andrew and Beatrice each have their own savings account. Beatrice’s account has $600 less than three times what Andrew’s account has. If Andrew had $300 more dollars, then he would have exactly half what is currently in Beatrice’s account. How much does Beatrice have?” (1)

Lời giải.

Với câu hỏi này, chúng ta có thể đặt 2 ẩn như sau:

a: số tiền tiết kiệm của Andrew

b: số tiền tiết kiệm của Beatrice

Dựa trên dữ liệu bài cho, chúng ta có thể thiết lập hệ phương trình:

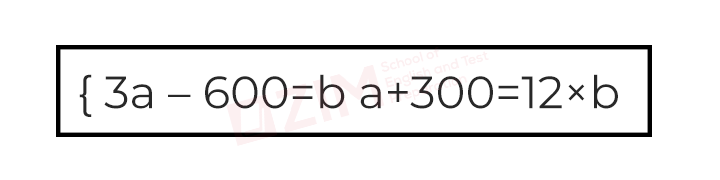
Từ đây, chúng ta dễ dàng tìm ra giá trị của b là 3000 và kết luận rằng Beatrice có $3000 trong tài khoản tiết kiệm.

Tính chất của số nguyên và số học (Integer Properties & Arithmetic)

a) Thừa số và bội số; Mẫu chung nhỏ nhất và Ước chung lớn nhất

b) Thương số và phần dư

c) Số chẵn và số lẻ

d) Số nguyên tố

e) Các số hạng liên tiếp và các dãy số (số chẵn, số lẻ, bội của 5)

f) Các tính chất đặc biệt của số 1 (ví dụ: tích của 1 với bất kỳ số nào sẽ bằng chính nó)

g) Các tính chất đặc biệt của số 0 (ví dụ: mọi số cộng với 0 đều bằng chính nó)

Ví dụ.

“How many integral divisors does the number 120 have? A. 14 B. 16 C. 12 D. 20 E. None of these” (2)

Lời giải.

Để giải bài toán trên, chúng ta phân tích thừa số nguyên tố cấu tạo nên số 120 như sau:

Chúng ta thấy số mũ của các thừa số lần lượt là 3, 1, 1. Từ đó, có thể suy ra được số các số bị chia a là số bị chia (divisor). Theo đề bài, chúng ta có thể suy ra được số ước của 120 là:

4×2×2=16

→ Chọn đáp án B.

Đại số (Algebra)

Trong phần này, các vấn đề đòi hỏi thí sinh có khả năng làm việc với các khái niệm sau:

a) Làm việc với phương trình, bao gồm phân phối và số âm;

b) Giải phương trình và bất phương trình 1 ẩn;

c) Phương trình bậc 2;

d) Phương trình và hệ phương trình đa ẩn;

e) Phương trình có chứa dấu căn;

Ví dụ.

“If x > 0, how many integer values of (x,y) will satisfy the equation 5x+4|y|=55?
A. 3
B. 6
C. 5
D. 4
E. Infinitely many” 

Lời giải.

Với đề bài trên, chúng ta có thể giải phương trình như sau:

Ta có: 

Vì x>0, |y|≥0 và x, y là số nguyên (integer) nên các giá trị của x chỉ có thể thuộc các số từ 1 đến 11. Tuy nhiên, ta có thể thấy kết quả của phép tính (55 ─ 5x) sẽ là 1 số chia hết cho 5. Mà trong các số hạng bé hơn 55, chỉ có 3 số vừa chia hết cho đồng thời 4 và 5, đó là 0, 20 và 40.

Trường hợp 1: 55 ─ 5x=0 → |y|=0 và x=11 

→ Có 1 cặp giá trị (x, y) là (11, 0).

Trường hợp 2: 55 ─ 5x=20 → |y|=5 và x=7

→ Có 2 cặp giá trị (x, y) là (7, 5) và (7,─ 5).

Trường hợp 3: 55 ─ 5x=40 → |y|=10 và x=3 

→ Có 2 cặp giá trị (x, y) là (3, 10) và (3,─ 10).

Vậy có tất cả 5 cặp giá trị (x, y) thỏa mãn yêu cầu bài toán.

→ Chọn đáp án C.

Phần trăm, Tỉ lệ thức và Phân số (Percent, Ratios & Fractions)

Ở phần này, thí sinh sẽ được yêu cầu giải quyết các vấn đề bao gồm những khái niệm cơ bản về phần trăm, tỉ lệ và phân số. Ta có thể xem xét ví dụ dưới để hình dung cụ thể hơn hình thức của dạng bài này.

Ví dụ.

“If 28 passes to a show cost $420, then at the same rate, how much will 42 passes cost? (A) $500
(B) $560
(C) $630
(D) $700
(E) $840″ (6)

Lời giải.

Với dạng bài này, gọi x ($) là số tiền cần chi trả cho 42 lượt đến buổi biểu diễn. Ta có thể tóm tắt lại như sau:

28 lượt: $420

42 lượt: $x

Thật vậy, bài toán có thể được giải bằng cách dựa vào tỉ lệ sau:

→ Chọn đáp án C.

Hình học phẳng (Two Dimensional Geometry)

Ở phần này, các dạng bài sẽ đòi hỏi thí sinh giải các bài toán dựa vào những kiến thức hình học phẳng, bao gồm đường thẳng, góc, tam giác, tứ giác, hình tròn, tính chu vi, diện tích các hình đề bài cho.

Ví dụ.

“What is the radius of the incircle of the triangle whose sides measure 5, 12 and 13 units?
A. 2 units
B. 12 units
C. 6.5 units
D. 6 units
E. 7.5 units” (7)

Lời giải.

Ví dụ trên yêu cầu tính bán kính đường tròn nội tiếp tam giác có số đo 3 cạnh lần lượt là 5, 12 và 13 đơn vị. Ta thấy:

Từ đó, theo định lý Pytago đảo, ta có thể suy ra được tam giác đã cho là tam giác vuông có cạnh huyền là 13 đơn vị.

Gọi a,b lần lượt là 2 cạnh góc vuông của tam giác, a=5, b=12.

Gọi p là số đo nửa chu vi của tam giác → p=15.

Gọi r là độ dài bán kính đường tròn nội tiếp tam giác.

Gọi S là diện tích tam giác vuông.

Ta có công thức tính diện tích tam giác như sau:

Những chủ đề ít gặp

Thống kê (Statistics)

Ở phần này, các bài toán đòi hỏi thí sinh phải làm việc với các khái niệm cơ bản về thống kê. Trong đó, 4 khái niệm quan trọng bao gồm:

• Mean: Trung bình cộng, được tính bằng cách lấy tổng của tất cả các số hạng chia cho số các số hạng đó.

• Median: Khi ta sắp xếp các số trong dãy theo thứ tự tăng dần, median có giá trị bằng số chính giữa của dãy. Nếu dãy số có số các số hạng là số chẵn, median có giá trị bằng trung bình cộng 2 số hạng giữa của dãy.

• Range: Trong dãy số, range được tính bằng hiệu của số lớn nhất và số nhỏ nhất của dãy. Vì vậy, range luôn mang giá trị dương.

• Standard Deviation (Độ lệch chuẩn): Theo Wikipedia, độ lệch chuẩn “là một đại lượng thống kê mô tả dùng để đo mức độ phân tán của một tập dữ liệu đã được lập thành bảng tần số.” Công thức tính độ lệch chuẩn như sau:

Lũy thừa và căn thức (Power & Roots)

Ở phần này, thí sinh cần trả lời các câu hỏi liên quan đến số mũ và căn. Tuy nhiên, vì không được dùng máy tính nên các giá trị lũy thừa hoặc căn thức sẽ ở mức độ thí sinh có thể tính nhẩm được. Dưới đây là một số cách đọc các phép tính lũy thừa và căn thức:

Xác suất và Tổ hợp (Probability & Combinatronics)

Xác suất (Probability): Ở dạng bài này, thí sinh có thể được yêu cầu xác định không  gian mẫu để có thể tính ra được khả năng xảy ra biến cố cần tìm. Xác suất để biến cố A xảy ra thường được ký hiệu là P(A), 0 ≤ P(A) ≤ 1.

Tổ hợp (Combinatronics): Ở dạng bài này, thí sinh sẽ được yêu cầu xác định số khả năng xảy ra các trường hợp thỏa mãn những tiêu chí cụ thể, bao gồm phép đếm (bao gồm quy tắc nhân và quy tắc cộng), hoán vị (Pn) và tổ hợp (Cnk).

Bất đẳng thức (Inequalities)

GMAT cũng yêu cầu thí sinh có khả năng giải quyết các bài toán liên quan đến bất đẳng thức, nhưng chỉ ở mức cơ bản như đã được học ở chương trình Trung học phổ thông. Các câu hỏi chủ yếu yêu cầu thí sinh xác định tập giá trị của x để biểu thức đã cho sẽ có giá trị dương (be positive) hoặc giá trị âm (be negative).

Dãy số (Sequences)

Đối với dạng bài này, các câu hỏi chủ yếu sẽ đòi hỏi thí sinh có kiến thức căn bản về cấp số cộng để tìm ra quy luật của dãy số và giá trị tiếp theo của dãy. Bạn có thể lưu lại công thức cấp số cộng dưới đây để giải quyết bài toán về dãy số:

Hình học Tọa độ (Coordinate Geometry)

Để giải quyết những bài toán dạng này, thí sinh cần nắm được những khái niệm cơ bản về mặt phẳng tọa độ, trục tung (Ox) và trục hoành (Oy), gốc tọa độ, xác định tọa độ các điểm và tính được khoảng cách giữa 2 điểm trên mặt phẳng khi biết tọa độ của 2 điểm đó.

Thông hiểu dữ liệu (Data interpretation)

Dạng bài này đòi hỏi thí sinh có thể hiểu được dữ liệu thông qua nhiều hình thức biểu diễn khác nhau, bao gồm các dạng biểu đồ đường, biểu đồ tròn, biểu đồ cột, và bảng giá trị. Từ đó, thí sinh có thể tính giá trị trung bình hoặc so sánh sự thay đổi của dữ liệu qua các biểu đồ.

Hình học không gian (Three dimensional objects)

Đối với dạng bài Hình học không gian, thí sinh chỉ cần nắm được những khái niệm cơ bản để tính các số đo khoảng cách, chu vi, diện tích, thể tích của các hình khối như hình hộp chữ nhật, hình lập phương, hình trụ.

Hàm số (Functions)

Hàm số y = f(x) được dùng để diễn tả mối quan hệ giữa giá trị của các biến x và y. Trong bài thi GMAT, thí sinh có thể cần làm việc với nhiều hàm số để giải một bài toán cụ thể. Vì vậy, những kiến thức cơ bản về tính chất của hàm số như cộng, trừ, nhân, chia đã được học ở chương trình cấp 3 sẽ giúp ích cho thí sinh rất nhiều trong quá trình làm bài.

Lưu ý: Các kiến thức về Tích phân (Calculus) và Lượng giác (Trigonometry) sẽ không bao gồm trong phần Quantitative Section GMAT.

Nguồn: Complete Guide to the GMAT by Magoosh

Tổng hợp thuật ngữ Toán Hình Học trong Quantitative Section GMAT(8)

Phùng Thị Anh Thy