Special right triangles - Ứng dụng trong SAT Math và chiến lược làm bài

Trong phần hình học của kỳ thi SAT Math, việc sử dụng thành thạo các tam giác vuông đặc biệt (special right triangles) — như tam giác 45°-45°-90° và 30°-60°-90° — có thể tạo ra lợi thế lớn về tốc độ và độ chính xác. Dù thí sinh đã nắm vững kiến thức hình học cơ bản, nhưng khi gặp các bài toán phức tạp hơn — tam giác lồng trong đa giác, kết hợp tỷ lệ cạnh hay hình chiếu — rất nhiều học sinh vẫn cảm thấy lúng túng trong cách áp dụng tỷ lệ cạnh đúng. Bài viết này sẽ giúp người đọc hiểu rõ khái niệm, nhớ các tỷ lệ cạnh nổi bật, đồng thời cung cấp chiến lược giải nhanh và thực hành bài tập mẫu để bạn tự tin cải thiện điểm phần hình học SAT Math.

Special Right Triangles là gì?

Special right triangles là các tam giác vuông có góc đặc biệt và tỷ lệ cạnh cố định, giúp người học tính nhanh các cạnh mà không cần dùng công thức Pythagoras mỗi lần [1]. Hai loại phổ biến nhất là tam giác 45°-45°-90° và tam giác 30°-60°-90°.

Tính chất:

• Tam giác 45°-45°-90°: hai cạnh góc vuông bằng nhau, cạnh huyền bằng cạnh góc vuông nhân √2.

• Tam giác 30°-60°-90°: cạnh đối góc 30° ngắn nhất (short leg), cạnh đối góc 60° dài hơn gấp √3 lần, và cạnh huyền gấp đôi cạnh ngắn nhất [2].

Những tỷ lệ cố định này giúp thí sinh xác định nhanh độ dài các cạnh khi biết một cạnh, đặc biệt hữu ích trong SAT Math nơi thời gian làm bài rất giới hạn.

Ôn tập thêm: Cách làm dạng bài Geometry and Trigonometry trong SAT Math & Bài tập

Các công thức quan trọng của Special Right Triangles

Công thức tỷ lệ cạnh của hai loại tam giác đặc biệt được trình bày như sau:

Với tam giác 45°-45°-90°:

• Nếu mỗi cạnh góc vuông có độ dài x, thì cạnh huyền (hypotenuse) = \(x\sqrt2\).

• Ngược lại, nếu cạnh huyền = h thì mỗi cạnh góc vuông = \(\frac{h}{\sqrt2}\)hoặc \(\frac{h\sqrt2}{2}\) .

Với tam giác 30°-60°-90°:

• Nếu cạnh đối góc 30° = x, thì cạnh đối góc 60° = \(x\sqrt3\) và cạnh huyền = 2x.

• Nếu cạnh huyền = h, thì short leg = \(\frac{h}{2}\) và long leg = \(\frac{h\sqrt3}{2}\).

Các công thức này cho phép thí sinh tính nhanh cạnh còn lại khi biết một cạnh bất kỳ, thay vì phải áp dụng toàn bộ định lý Pythagoras.
Ví dụ:

• Một hình vuông có cạnh bằng 4 → đường chéo chia hình thành hai tam giác 45°-45°-90° → đường chéo = \(4\sqrt2\).

• Một tam giác đều cạnh 10 khi chia đôi tạo ra tam giác 30°-60°-90° → chiều cao = \(\frac{10\sqrt3}{2}\).

Ứng dụng Special Right Triangles trong bài toán SAT Math

Các bài hình học trong SAT Math thường xuất hiện dạng tam giác đặc biệt dưới nhiều hình thức khác nhau: tam giác đơn, hình ghép, hoặc bài toán không gian.

1. Nhận diện nhanh hình dạng:
Khi đề bài xuất hiện góc 30°, 45° hoặc 60°, hoặc đề cập đến đường chéo hình vuông hay đường cao trong tam giác đều, điều đó gợi ý có một special right triangle. Việc nhận diện đúng hình dạng giúp tiết kiệm đến 30% thời gian làm bài.

2. Áp dụng tỷ lệ cạnh:
Ví dụ:

Trong tam giác vuông, nếu góc nhỏ nhất là 30° và cạnh đối góc 30° = 5, hãy tìm cạnh huyền.
Áp dụng ngay tỷ lệ 1 : \(\sqrt3\) : 2 → hypotenuse = 10, long leg = \(5\sqrt3\).

3. Tích hợp trong hình phức hợp:
Nhiều bài SAT không trình bày tam giác rõ ràng mà ẩn nó trong hình chữ nhật, lăng trụ hoặc đa giác. Khi nhận diện được tam giác đặc biệt, thí sinh có thể “tách” phần cần tính và sử dụng tỷ lệ cạnh để giải nhanh.

4. Kết hợp với tỉ số và tương đồng:
Trong các bài có hai tam giác đồng dạng, nếu một trong số đó là special right triangle, tỷ lệ cạnh được dùng để tìm cạnh còn lại nhanh chóng mà không cần nhiều phép tính.

Chiến lược giải bài tập SAT nhanh và chính xác

Để đạt điểm cao trong phần Geometry của SAT Math, thí sinh cần vận dụng bốn chiến lược trọng tâm:

Chiến lược 1 – Nhận diện ngay khi đọc đề:
Mỗi khi thấy tam giác có góc 30°, 45°, hoặc 60°, cần xác định xem đó có phải special right triangle hay không. Việc nhận ra dấu hiệu đặc trưng này là bước đầu tiên để rút ngắn quá trình tính toán.

Chiến lược 2 – Ghi nhớ và viết lại tỷ lệ cạnh:
Trước khi bắt đầu giải, nên viết ngay tỷ lệ cạnh:

• 45°-45°-90° → 1 : 1 : \(\sqrt2\)

• 30°-60°-90° → 1 : \(\sqrt3\) : 2
  Việc viết công thức ra giấy giúp hạn chế nhầm lẫn, đặc biệt trong các bài hình phức tạp.

Chiến lược 3 – Loại trừ đáp án sai:
Trong đề trắc nghiệm, nếu một đáp án không đúng với tỷ lệ cạnh của tam giác đặc biệt, có thể loại bỏ ngay. Chiến lược này giúp tiết kiệm thời gian và giảm rủi ro chọn nhầm.

Chiến lược 4 – Kết hợp với bài toán phức hợp:
Nhiều câu hỏi SAT yêu cầu tính diện tích, độ cao, hoặc phần còn lại của hình lớn hơn. Khi tách hình đó thành special right triangles, việc tính toán trở nên nhanh và chính xác hơn.

Chiến lược 5 – Luyện phản xạ bằng bài tập thực tế:
Luyện thường xuyên các bài dạng “tam giác đặc biệt ẩn” trong hình ghép hoặc đồ thị giúp tăng tốc độ nhận diện trong phòng thi.

Từ vựng cần thiết khi làm bài tập dạng Special right triangles

Khi làm bài thi SAT, việc hiểu rõ từ vựng chuyên môn giúp thí sinh đọc và phân tích đề nhanh hơn.
Một số thuật ngữ quan trọng thường gặp trong các câu hỏi về special right triangles [3]:

• Special right triangle – tam giác vuông đặc biệt.
  Example: “Recognize a special right triangle in the diagram to find missing sides.”

• Leg – cạnh góc vuông trong tam giác vuông.
  Example: “Each leg in a 45-45-90 triangle is equal in length.”

• Hypotenuse – cạnh huyền, cạnh dài nhất đối diện góc vuông.
  Example: “In a 30-60-90 triangle, the hypotenuse is twice the short leg.”

• Short leg / Long leg – cạnh ngắn và cạnh dài trong tam giác 30-60-90.
  Example: “The short leg is opposite the 30° angle.”

• Ratio – tỷ lệ giữa các cạnh.
  Example: “The ratio of the sides in a 45-45-90 triangle is 1:1:√2.”

• Recognize – nhận diện.
  Example: “Recognize patterns of special triangles to solve faster.”

Việc làm quen và ghi nhớ nhóm từ vựng này giúp thí sinh hiểu đề nhanh, đặc biệt với các câu hỏi mô tả hình học bằng ngôn ngữ học thuật.

Xem thêm: Tổng hợp từ vựng SAT Math theo chủ đề [PDF]

Bài tập thực hành

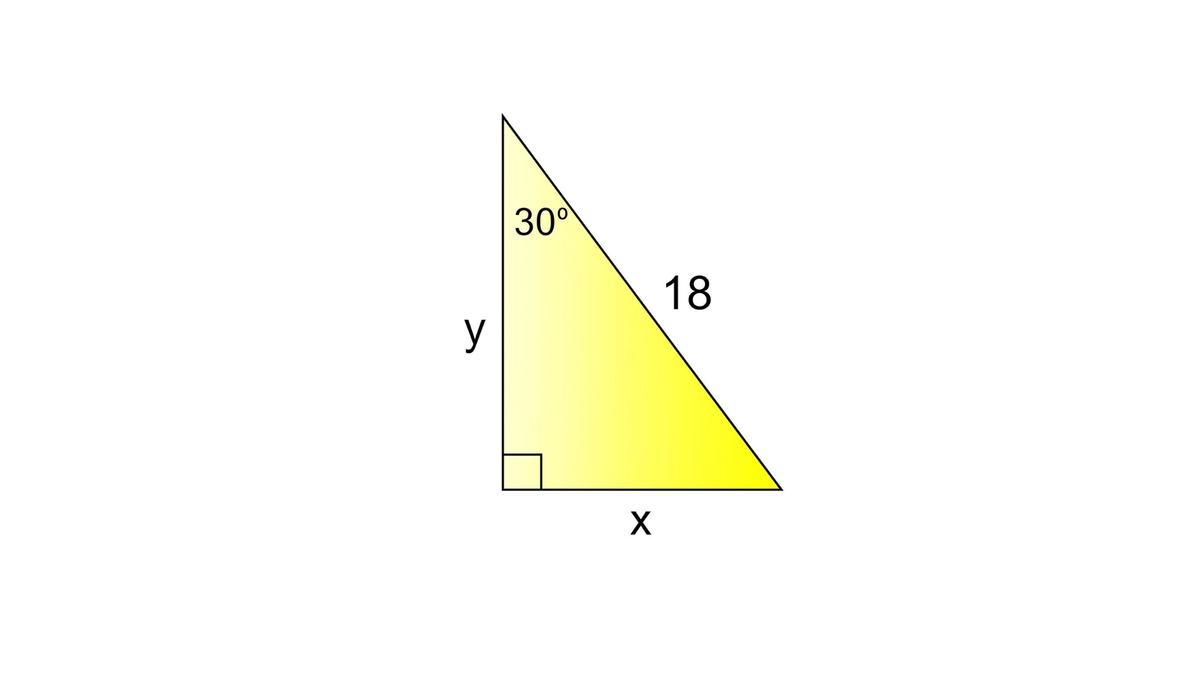
Bài 1: Tam giác 30°–60°–90°

Given the diagram, as labeled, find x and y.

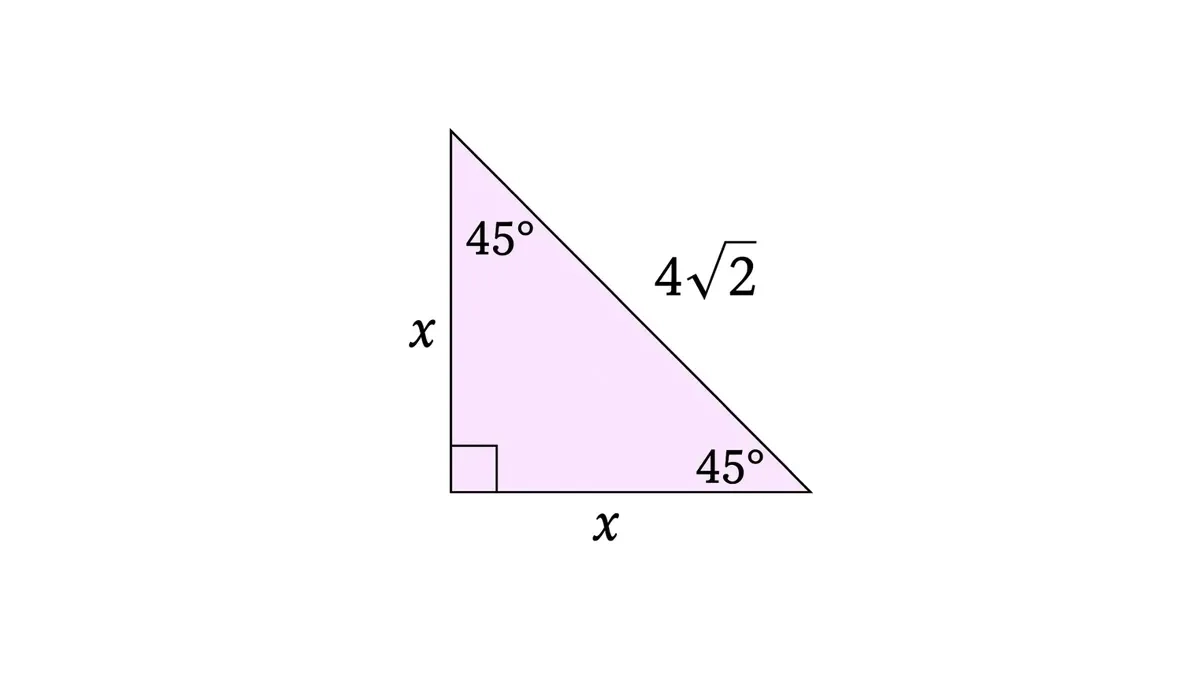
Bài 2: Tam giác 45°–45°–90°

Given the diagram, as labeled, find x.

Lời giải tham khảo

Bài 1:
Trong tam giác 30°–60°–90°:

short leg : long leg : hypotenuse = 1 : \(\sqrt3\) : 2

Cho cạnh huyền =18. Đặt short leg =x (đối góc 30°), khi đó:

2x = 18 ⇒ x=9

Cạnh dài y = \(x\sqrt3\) ⇒ y = \(9\sqrt3\)

Kết luận: x=9, y = \(9\sqrt3\)

Bài 2:
Trong tam giác 45°–45°–90:
leg : leg : hyp = 1 : 1 : \(\sqrt2\).
Đặt mỗi cạnh góc vuông = x ⇒ cạnh huyền = x\(\sqrt2\) .
Cho x\(\sqrt2\) = 4\(\sqrt2\) ⇒ x = 4 .

Tìm hiểu thêm: Right triangle trigonometry SAT math - Tỉ số lượng giác tam giác vuông

Tổng kết

Trong phần hình học của SAT Math, việc nắm vững special right triangles là chìa khóa để giải nhanh và chính xác các bài toán liên quan đến tam giác, đa giác và hình không gian. Chúng là các tam giác có tỷ lệ cạnh cố định, cho phép giải nhanh mà không cần dùng định lý Pythagoras. Thí sinh cần nắm rõ hai loại: tam giác 45°-45°-90° (với tỷ lệ cạnh x : x : \(x\sqrt2\) ) và tam giác 30°-60°-90° (với tỷ lệ x : \(x\sqrt3\) : 2x cho các cạnh đối góc 30°, 60° và 90°). Việc áp dụng nhanh các công thức này giúp chuyển đổi bài toán hình học phức tạp thành các phép tính đơn giản, tối ưu hóa thời gian làm bài thi.

Để giúp thí sinh giải quyết các dạng toán hiệu quả trong bài thi SAT Math, đội ngũ chuyên môn tại ZIM đã biên soạn tựa sách Think in SAT Digital Math - Reasoning and Strategies. Với mỗi dạng bài, cuốn sách sẽ cung cấp kiến thức cơ bản, các ví dụ, cách giải mẫu và bài tập. Đọc thử tại đây.

Tác giả: Lê Minh Bảo Trân