Sử dụng DESMOS để tìm phương trình tuyến tính qua toạ độ hai điểm

Trong các bài thi chuẩn hóa quốc tế về năng lực toán, chẳng hạn như Digital SAT, thí sinh có thể sẽ được cung cấp phần mềm DESMOS, phần mềm máy tính khoa học giúp giải quyết các vấn đề liên quan đến đồ thị, thống kê, và các phép tính cơ bản. Bài viết này sẽ hướng dẫn người đọc cách sử dụng DESMOS để tìm phương trình tuyến tính qua tọa độ hai điểm, một dạng bài phổ biến trong bài thi Digital SAT. Nắm được các tính năng của DESMOS cũng như thao tác sử dụng sẽ giúp thí sinh tăng tốc độ làm bài, đơn giản hoá các bước tính toán, từ đó nâng cao hiệu quả bài thi.

Lý thuyết về phương trình tuyến tính thông qua tọa độ hai điểm

Nếu ta có hai điểm A(x1, y1) và B(x2, y2), thì phương trình tuyến tính đi qua hai điểm này có dạng slope-intercept là:

y = mx + b

Trong đó: 

• m là hệ số góc của phương trình, có công thức là

  \[m=\frac{y{}2{}-y1}{x2-x1}\]

• Ngoài ra, b là hệ số tự do của phương trình.

Phương trình tuyến tính cũng có thể được viết dưới dạng tổng quát (standard) là:

Ax + By = C

Trong đó: 

• -A/B là hệ số góc của phương trình (với B ≠ 0)

• A, B và C là các hằng số, với A và B không đồng thời bằng 0

Cách tìm phương trình tuyến tính thông qua tọa độ hai điểm 

Để tìm phương trình tuyến tính thông qua tọa độ hai điểm, ta trước hết sẽ phải tìm được hệ số góc m theo công thức trên bằng việc thế các giá trị (x, y) của 2 điểm được cho. Sau khi có được hệ số góc m, ta sau đó tìm b bằng cách thế tọa độ một điểm vào phương trình y = mx + b.

Ví dụ: Ví dụ, cho hai điểm A(1, 2) và B(3, 6)

Trước hết, ta tính hệ số góc m của đường thẳng đi qua hai điểm A và B theo công thức:

\[m=\frac{y{}2{}-y1}{x2-x1}\]

Lưu ý, công thức này cần điều kiện là x₁ ≠ x₂ (hai điểm không có cùng hoành độ, tức đường thẳng không song song với trục tung).

Thế tọa độ hai điểm vào công thức, ta được:

\[m=\frac{6-2}{3-1}=2\]Sau khi tìm được hệ số góc m = 2, ta thay tọa độ một trong hai điểm (chẳng hạn điểm A(1, 2) vào phương trình y = mx + b để tìm b:

2 = 2 x 1 + b  -> b = 0

Vậy phương trình tuyến tính đi qua hai điểm A và B là: y = 2x

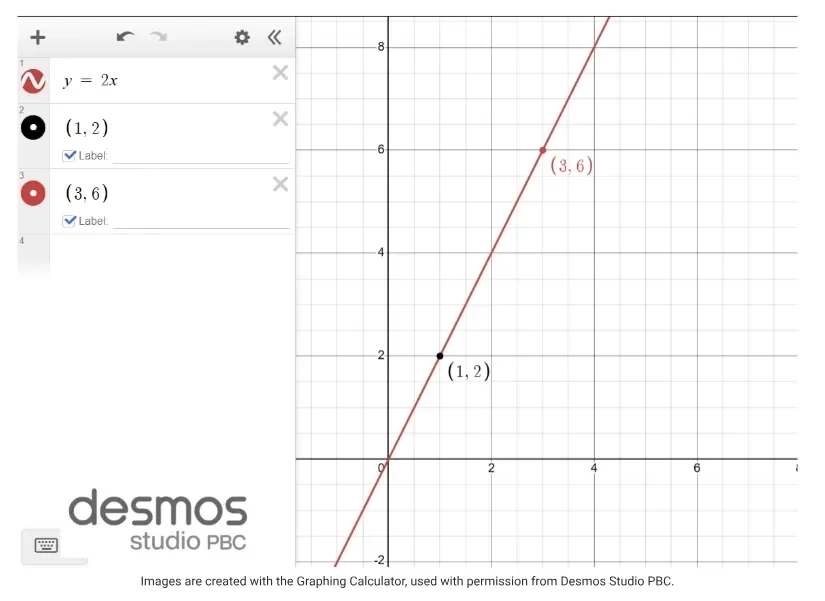
Fig. 1. Line y = 2x on the Desmos Graphing Calculator. (Source [1])

Phương trình tuyến tính thông qua tọa độ hai điểm trong câu hỏi Digital SAT

Trong bài thi Digital SAT, các câu hỏi về việc tìm phương trình tuyến tính thông qua tọa độ hai điểm rất đa dạng. Thí sinh có thể được hỏi về việc tìm phương trình tuyến tính trực tiếp từ hai điểm đã cho, xác định hệ số góc của đường thẳng, tìm tung độ gốc, hoặc viết phương trình dưới các dạng khác nhau.

Giới thiệu máy tính khoa học DESMOS

DESMOS là một phần mềm máy tính khoa học được thiết kế bởi DESMOS Studio. Đây là phần mềm chính thức được tích hợp trong phần mềm Bluebook của bài thi Digital SAT nhằm hỗ trợ thí sinh giải quyết đa dạng câu hỏi Toán học ở nhiều chuyên đề khác nhau.

Fig. 2. Official logo of Desmos Studio PBC. (Source: [2])

Các tính năng cơ bản của DESMOS

Với phần mềm DESMOS, người học và thí sinh sẽ cần làm quen với một số tính năng cơ bản, bao gồm:

• Các phép cộng, trừ, nhân, chia cơ bản

• Vẽ đồ thị phương trình từ bậc thấp đến cao

• Sử dụng bảng biểu

• Tính năng thanh trượt

• Các phép tính thống kê cơ bản

• Các phép tính lượng giác cơ bản

• V.v.

Trên màn hình giao diện DESMOS, người học có thể nhận diện được các vùng cơ bản. Thứ nhất, vùng bên tay trái là nơi người học nhập phương trình (VD: 2x + y = 0). Thứ hai, vùng mặt phẳng toạ độ Oxy là nơi đồ thị của phương trình hiển thị. Cuối cùng, nút cài đặt (có biểu tượng hình cờ lê) bên góc phải là nơi người học điều chỉnh một số cài đặt để phù hợp nhu cầu (VD: chuyển đổi từ Degree sang Radian.)

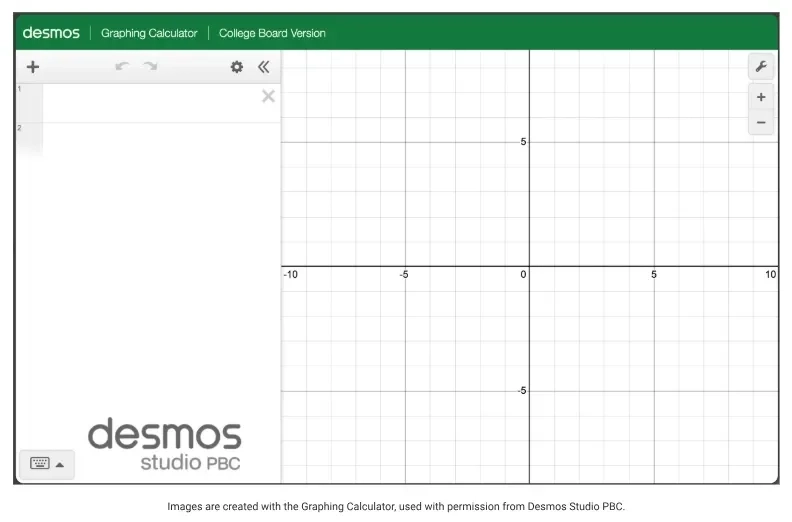
Fig. 3. Interface of the Desmos Graphing Calculator. (Source: [3])

Lưu ý: Phần mềm DESMOS hiện tại mà người học có thể tìm trên mạng có thể được chia làm hai phiên bản: Nguyên bản (đen) và Khảo thí (testing - xanh lá). Phần mềm DESMOS nguyên bản sẽ có nhiều tính năng hơn bản khảo thí, bao gồm tính năng chia sẻ biểu đồ, thư mục, hoặc hình ảnh. Tuy vậy, các tính năng quan trọng dùng trong bài thi SAT vẫn có đầy đủ ở cả hai phiên bản.

Hướng dẫn sử dụng DESMOS để tìm phương trình tuyến tính qua tọa độ hai điểm

Để sử dụng DESMOS để tìm phương trình tuyến tính thông qua tọa độ hai điểm, người học cần vận dụng tính năng vẽ đồ thị phương trình và lập bảng (table). Dưới đây là hướng dẫn chi tiết từng bước:

Bước 1: Đọc kĩ đề để xác định dữ kiện được cung cấp.

Người học đọc kĩ phương trình để xác định toạ độ của 2 điểm được đề bài cho cũng như là xác định đề bài đang yêu cầu người học tìm gì.

Bước 2: Người học cần mở chức năng table bằng cách bấm vào dấu cộng để “add item”. Sau đó, người học cần nhập dữ kiện được cung cấp từ đề bài (toạ độ điểm) vào ô nhập dữ liệu của phần bảng trong DESMOS graphing calculator. Chức năng bảng này sẽ giúp người học điền được toạ độ của mọi điểm đề bài cho.

DESMOS sẽ tự động cho thấy các điểm này trên mặt phẳng toạ độ.

Bước 3: Người học có thể thấy một biểu tượng đường thẳng ở trên giao diện, và khi rê chuột đến biểu tượng này sẽ thấy dòng chữ “add regression”. Người học bấm vào biểu tượng này để DESMOS vẽ đường thẳng và cho người học thấy phương trình tuyến tính đi qua hai điểm được cho.

Sau khi nhấn vào "add regression" thì Desmos sẽ cho người học một giao diện với các dạng regression để người học chọn. Desmos sẽ để mặc định là "Linear Regression" và đây chính là dạng người học cần dùng, vì đây là phương trình tuyến tính.

Lưu ý: DESMOS luôn hiển thị giá trị dưới dạng số thập phân. Do đó, DESMOS sẽ hiện hệ số góc dạng phân số dưới dạng số thập phân (VD: 10/3 có thể được biểu diễn là 3.33333). Nếu vậy, người học nên luôn kiểm tra lại bằng việc viết hệ số góc của các đáp án vào DESMOS để các giá trị này được biến đổi thành dạng thập phân, giúp cho người học lựa chọn chính xác.

Bước 4: (tuỳ chọn) Thử lại tọa độ hai điểm vào trong đáp án để xét tính chính xác.

Ví dụ minh hoạ:

Câu hỏi: 

A line passes through the points (2, −1) and (6, 7). 

Which equation represents this line?

A. y = 2x − 5
B. y = x + 1
C. y = 3x − 7
D. y = 4x − 9

Hướng dẫn giải bằng DESMOS

Bước 1: Đọc kĩ đề để xác định dữ kiện được cung cấp

• Hai điểm: A(2, -1) và B(6, 7)

• Đề bài bắt tìm phương trình dưới dạng y = mx + b

Bước 2: Người học bắt đầu bằng việc tạo bảng.

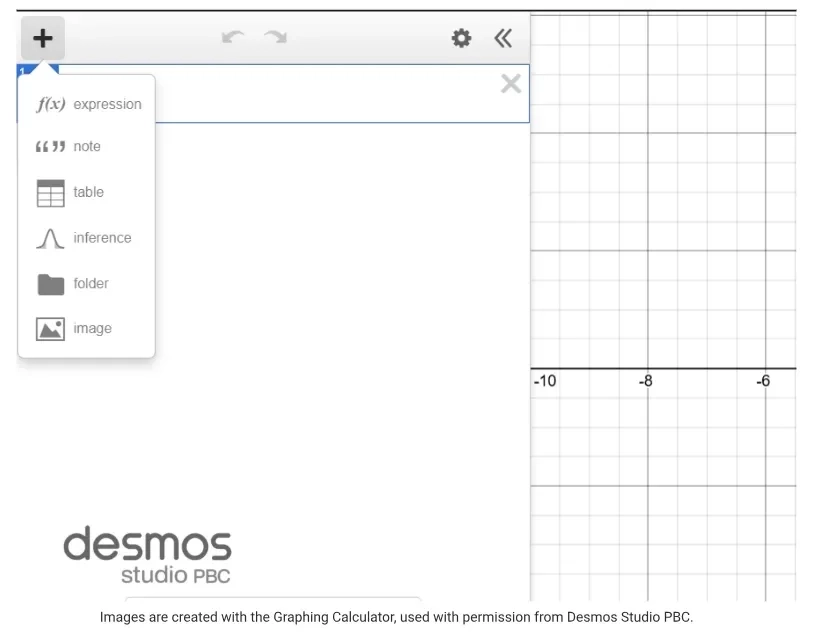
Fig. 4. Interface of the Desmos Graphing Calculator with the Table function. (Source: [4])

Sau đó, người học cần cho các toạ độ của điểm vào trong phần bảng đã lập được.

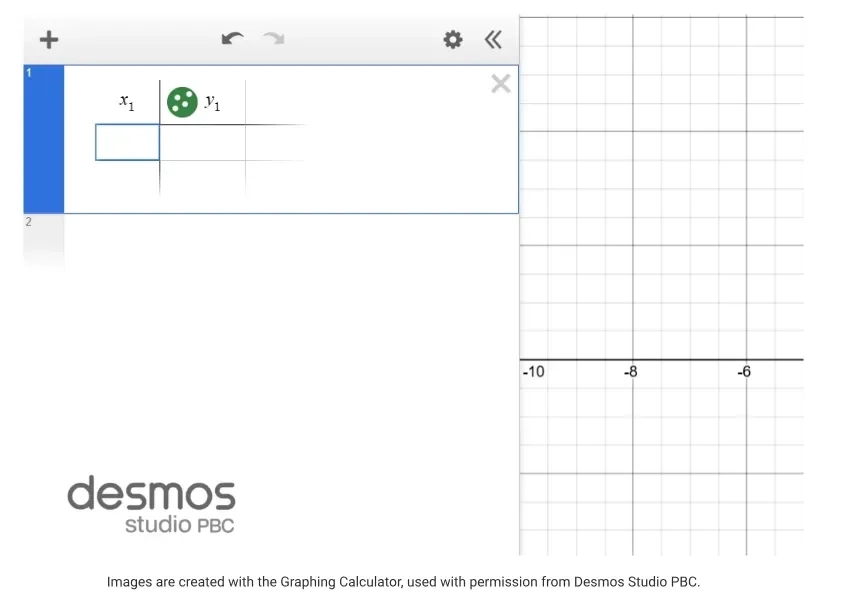
Fig. 5. The Table function of the Desmos Graphing Calculator. (Source: [5])

Người học nên có được một bảng hiện dữ liệu như sau.

Bước 3: DESMOS sẽ hiển thị hai điểm trên mặt phẳng tọa độ. Bây giờ người đọc bấm vào “add regression” để hiển thị đường thẳng đi qua hai điểm này.

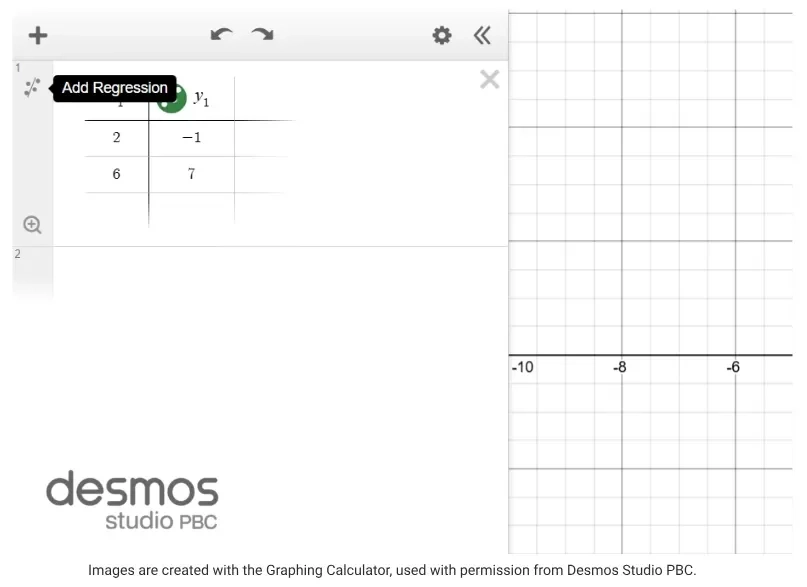
Fig. 6. The Add Regression function on the Desmos Graphing Calculator. (Source: [6])

Bây giờ, người học có thể thấy giao diện hiện “equation” là y = 2x - 5. 

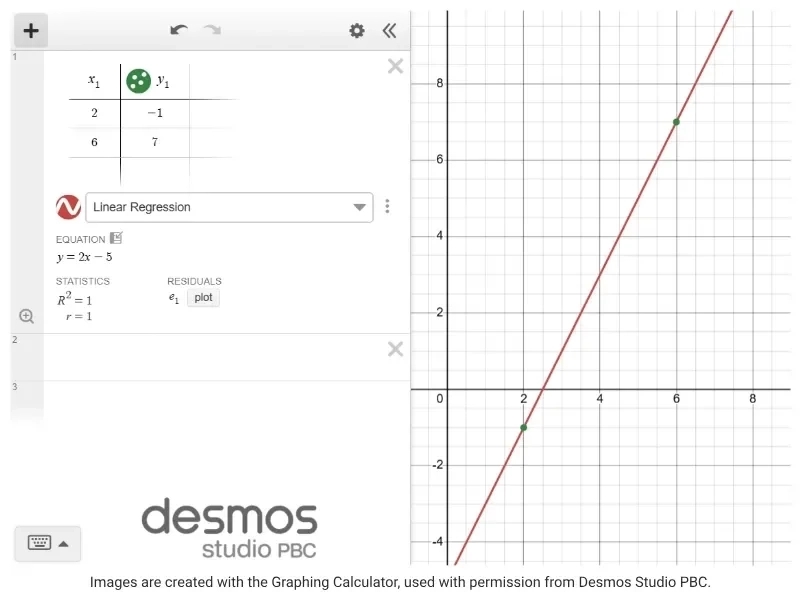
Fig. 7. Line y = 2x - 5 on the Desmos Graphing Calculator. (Source [7])

Bước 4: Thử lại toạ độ điểm vào hàm số tìm được để kiểm tra đáp án: 

• 2 x 2 - 5 = -1 (Đúng)

• 2 x 6 - 5 = 7 (Đúng)

=> Chọn đáp án A.

Lưu ý: DESMOS luôn hiển thị giá trị dưới dạng số thập phân. Do đó, DESMOS hữu dụng khi giá trị cần tìm là giá trị nguyên (1,2,3,...), giá trị thập phân hữu hạn (1.5, 2.5,...), giá trị thập phân vô hạn tuần hoàn (0.6666), hoặc giá trị thập phân không tuần hoàn thông dụng (3.141592). Nếu người học chưa quen nhận diện các giá trị này (VD: 10/3 có thể được biểu diễn là 3.33333), điều nên làm là luôn kiểm tra lại đáp án trước khi chọn.

Xem thêm:

• Sử dụng DESMOS để tìm hàm số tuyến tính, biết một điểm và hệ số góc

• Cách làm dạng bài Linear equations in one variable trong SAT Math

• Linear equation word problems SAT Math (bài toán về phương trình tuyến tính)

Bài tập vận dụng 

Sau đây bài viết sẽ giới thiệu đến người học một số câu hỏi Digital SAT có sử dụng DESMOS để tìm phương trình tuyến tính thông qua tọa độ hai điểm [8]. Người học hãy sử dụng tính năng DESMOS đã giới thiệu để giải các câu hỏi sau.

Question 1: 

A line passes through the points (2, 5) and (4, 1).

Which of the following is an equation of the line in standard form?

A. 2x + y = 9
B. x - 2y = -8
C. 2x + 2y = 12
D. 2x − y = −12

Answer: A

Question 2: 

A linear equation passes through the points (0, 7) and (6, 1)

Which statement best describes the equation of the line?

A. The slope is −7/6​, and the y-intercept is 0
B. The slope is positive, and the y-intercept is 1
C. The slope is −1, and the y-intercept is 6 
D. The slope is negative, and the y-intercept is 7

Answer: D

Question 3:

Which equation represents a line that passes through both (-3, 4) and (3, 10)?

A. y = 2x + 4
B. y = x + 7
C. y = x + 1
D. y = 3x + 1

Answer: B

Question 4:

The graph of a line includes the points (-4, 1) and (2, -5).

Which of the following is the slope of the line?

A. -2
B. -3/2
C. -1
D. 3/2

Answer: C

Question 5:

A line passes through the points (4, -1) and (8, 7).

Which of the following equations does NOT represent this line?

A. y = 2x − 9
B. 2x - y = 9
C. y + 1 = 2(x - 4)
D. y = -2x + 15

Answer: D

Question 6:

A table shows values from a linear function.

Which equation represents the function?

A. y = −2x + 3
B. y = −x + 4
C. y = −2x + 7
D. y = x - 2

Answer: A

Question 7:

A line passes through the points A(1/2, 5/3) and B(7/2, 1/3)

Which equation represents this line?

A. \(y=-\frac49x+2\)
B. \(y=-\frac49x+\frac{17}{9}\)
C. \(y=-\frac23x+\frac{17}{9}\)
D. \(y=\frac23x+1\)

Answer: B

Question 8:

A line passes through the points (a, 4) and (6, -2), where a ≠ 6.

The slope of the line is −1.

Which equation represents this line?

A. y = −x + 2
B. y = -x + 6
C. y = −x + 4
D. y = -x + 8

Answer: C

Question 9:

A line passes through the points (-1, 2) and (3, -6).

Which points below also pass through this line?

A. (0, 0), (2, 5)
B. (1, -2), (-3, 6)
C. (0, -2), (2, 0)
D. (0, 0), (4, 2)

Answer: B

Question 10:

A delivery drone flies at a constant altitude while moving horizontally. At 2 seconds after launch, the drone is 48 meters from the launch point. At 8 seconds after launch, it is 120 meters from the launch point.

Which equation best models the distance d (in meters) from the launch point as a function of time t (in seconds)?

A. d = 12t + 24
B. d = 12t
C. d = 9t + 30
D. d = 15t - 18

Answer: A

Tổng kết

Như vậy, bài viết đã giới thiệu về phần mềm DESMOS và hướng dẫn chi tiết cách sử dụng DESMOS để tìm phương trình tuyến tính qua toạ độ hai điểm trong bối cảnh câu hỏi bài thi Digital SAT. Hi vọng người học có thể vận dụng các nội dung trong bài viết để cải thiện hiệu suất ôn tập và nâng cao hiệu quả làm bài của bản thân.

Để nâng cao kỹ năng làm bài Digital SAT một cách toàn diện, người học có thể tham gia khóa học SAT tại ZIM Academy. Chương trình cung cấp hướng dẫn chi tiết về chiến lược làm bài, sử dụng công cụ hiệu quả như DESMOS, và luyện tập với đề thi thực tế, giúp học viên tối ưu thời gian và đạt điểm số mục tiêu trong kỳ thi.