Congruence, similarity, and angle relationships - Cách làm và bài tập

Bài thi SAT Math đánh giá kiến thức ở nhiều phạm vi khác nhau, ngoài phần Đại số còn có cả Hình học và Lượng giác. Bài viết tập trung vào chiến lược giải quyết các câu hỏi thuộc chủ đề Congruence, Similarity, and Angle Relationships – tam giác đều, tam giác đồng dạng, và mối quan hệ giữa các góc. Mục tiêu là giúp người học nắm vững từng bước làm bài nhằm củng cố kiến thức và nâng cao kỹ năng cho kỳ thi SAT quan trọng.

Tổng quan về dạng bài Congruence, similarity, and angle relationships

Dạng bài Congruence, similarity, and angle relationships thuộc phần Geometry and Trigonometry của bài thi Toán học SAT và người học sẽ chọn trắc nghiệm đáp án A, B, C hoặc D. Phần thi có thể xuất hiện trong cả phần cho phép và không cho phép sử dụng máy tính. Nội dung thường nằm trong hai nhóm chính:

1. Lines and Angles: Các mối quan hệ về góc (Angle relationships).

2. Triangles and Other Polygons:

   • Các tam giác đều (Congruent triangles) và các hình đều khác.

   • Các tam giác đồng dạng (Similar triangles) và các hình đồng dạng khác. [1]

Những câu hỏi dạng này yêu cầu người học xác định giá trị chưa biết bằng cách vận dụng các mối quan hệ về góc, tam giác đồng dạng và giao điểm của các đường thẳng.

Chiến lược làm dạng bài Congruence, similarity, and angle relationships trong SAT Math

Tìm giá trị các góc trong hình tam giác

Để giải quyết dạng bài tìm giá trị các góc trong hình tam giác, người học cần ghi nhớ một số kiến thức cơ bản: [2]

• Tổng các góc trong của một tam giác luôn bằng 180 độ.

• Các góc trong tương ứng và góc so le trong bằng nhau khi có các đường thẳng song song.

• Các góc đối đỉnh luôn bằng nhau.

• Các góc bù nhau có tổng bằng 180 độ.

Bước 1: Dựa vào hình vẽ hoặc thông tin trong đề bài để xác định giá trị các góc đã cho.

Bước 2: Sử dụng các tính chất như góc đối đỉnh, góc bù nhau, hoặc tổng các góc trong tam giác để tính các góc còn lại.

Bước 3: Đề bài thường cung cấp các thông tin liên quan đến tính chất tam giác như parallel (song song), perpendicular (vuông góc), isosceles (tam giác cân), hoặc equilateral (tam giác đều). Những chi tiết này sẽ giúp xác định mối quan hệ giữa các góc dễ dàng hơn. 

Ví dụ hình tam giác được tạo thành bởi ba đường thẳng cắt nhau: Based on the figure above, what is the value of x?

1. Góc 121 độ và góc (1) là hai góc bù nhau, vì vậy:

Góc (1) = 180 - 121 = 59 độ

2. Tính góc (2) dựa trên tổng các góc trong tam giác:

Góc (2) = 180 - 59 - 29 = 92 độ

3. Góc (2) và góc (3) là góc đối đỉnh → Góc (3) = 92 độ

4. Tính góc (4) sẽ ra tổng các góc của tam giác bên phải

Góc (4) = 180 - 29 - 92 = 59 độ

5. Góc (4) và x là góc đối đỉnh → x = góc (4) = 59 độ

Xem thêm: Area and volume - Công thức, cách làm và bài tập vận dụng

Tìm cạnh trong tam giác đồng dạng

Một trong hình phổ biến của các tam giác đồng dạng là gồm hai đường thẳng song song và hai đường cắt nhau, như minh họa bên dưới.

Chiến lược giải quyết bài toán tam giác đồng dạng:

Bước 1: Chứng minh tam giác đồng dạng bằng cách kiểm tra các cặp góc tương ứng có bằng nhau hay không. Đây là cách đơn giản để khẳng định sự đồng dạng của tam giác.

Bước 2: Hãy sử dụng độ dài các cạnh đã biết để thiết lập phân số (tỷ lệ) giữa các cặp cạnh tương ứng. Ví dụ: Cạnh 1 của tam giác thứ nhất sẽ tỉ lệ với cạnh 1 của tam giác thứ hai, và tương tự với các cạnh còn lại. Giải giá trị các cạnh chưa biết bằng cách nhân chéo phân số. 

Bước 3: Sau khi đã tính được các cạnh, cần kiểm tra tỷ lệ các cạnh giữa hai tam giác là đồng nhất.

Ví dụ: In the figure below, AB is parallel to DE. If AC = 4, CD = 3 and BC = 5, what is the length of CE?

1. Góc CDE và góc CBA là các góc so le trong, vì vậy chúng là góc đồng dạng (congruent). Điều này chứng minh rằng tam giác ABC và tam giác EDC là đồng dạng.

2. Thiết lập tỷ lệ giữa tam giác ABC và tam giác EDC. Cụ thể:

\[\dfrac{BC}{DC}=\dfrac{CA}{CE}\]Thay các giá trị đã biết vào, ta có:  

\[\dfrac53=\dfrac{4}{CE}\]

Nhân chéo để giải: 5CE = 12 → CE = \(\dfrac{12}{5}=2\left(\dfrac25\right)\)

Tìm cạnh hoặc góc trong tam giác có cạnh đều (Congruence)

Bước 1: Xác định tam giác đều nhau dựa vào thông tin đề bài và các tiêu chí sau:

• SSS - Cả 3 cạnh của hai tam giác bằng nhau 

• SAS - 2  cạnh và góc xen giữa bằng nhau

• ASA - 2 góc và cạnh xen giữa bằng nhau

• AAS - 2 góc và một cạnh không xen giữa bằng nhau

• HL - Trong tam giác vuông, cạnh huyền và một cạnh góc vuông bằng nhau.

Hoặc dựa vào những tính chất của tam giác như isosceles (tam giác cân), hoặc equilateral (tam giác đều) sẽ suy ra được cạnh đều trong tam giác.

Bước 2: Sử dụng các số đo đã biết và tính chất của góc đối đỉnh, góc bù nhau, hoặc tổng các góc trong tam giác để tính các góc hoặc cạnh còn lại.

Ví dụ: In the figure above, triangle . That is, side AB is equal in length to side BC. Triangle DEF overlaps with triangle ABC. What is the value of p?

1. Vì tam giác

ABC cân với AB=BC nên hai góc A và C bằng nhau.

Đề bài cho góc B=100 độ. Người học áp dụng tính chất tổng ba góc trong tam giác bằng

2. Giả sử đặt góc A = góc C = x, ta có: x + x + 100 = 180 độ

→ 2x = 80 độ → x = 40 độ

3. Tính góc (1): 180 - 60 - 40 = 80 độ

Góc (1) và p là hai góc đối đỉnh nên chúng có số đo bằng nhau 

Vì vậy, p = 80 độ

Xem thêm: SAT Math formulas: Các công thức thường gặp trong SAT Math

Một số lưu ý

Tự đưa ra giả định

Một trong những sai lầm phổ biến mà người học thường mắc phải là vội vàng đưa ra giả định về lý thuyết hoặc công thức mà không chứng minh hoặc không có trong đề bài. Điều này dễ dẫn đến hiểu sai mối quan hệ giữa các góc, hoặc giữa tam giác đều và tam giác đồng dạng. Người học cần tránh suy đoán theo cảm tính, thay vào đó là tập trung chứng minh dựa trên các tiêu chí như số đo góc, tỷ lệ cạnh, các mối quan hệ góc bù, góc phụ được đề cập trong đề bài.

Nhầm lẫn giữa tam giác đều và tam giác đồng dạng

Tam giác đều và tam giác đồng dạng có một số đặc điểm giống nhau khiến nhiều người học áp dụng sai quy tắc hoặc công thức, từ đó mất điểm không đáng có. Để tránh lỗi này, người học cần nắm rõ lý thuyết về hai loại tam giác: 

• Tam giác đồng dạng có tỉ lệ cạnh bằng nhau và góc tương ứng bằng nhau

• Tam giác đều có cả ba cạnh và ba góc bằng nhau 

Ngoài ra người học cũng nên thực hành nhiều dạng bài tập để phân biệt thật tốt giữa hai loại tam giác này.

Không chú ý đến thông tin đã cho

Học sinh thường vội vã giải câu hỏi mà không phân tích đầy đủ thông tin hoặc manh mối nằm trong đề bài và trong hình. Mỗi thông tin trong đề bài đều có mục đích và đóng vai trò như một mảnh ghép quan trọng giúp tìm ra đáp án. Chỉ cần bỏ qua một chi tiết nhỏ cũng có thể khiến bài toán trở nên sai lệch. Do đó, học sinh nên luyện kỹ năng dành thời gian đọc kỹ đề bài và quan sát cẩn thận hình vẽ.

Bài tập ứng dụng

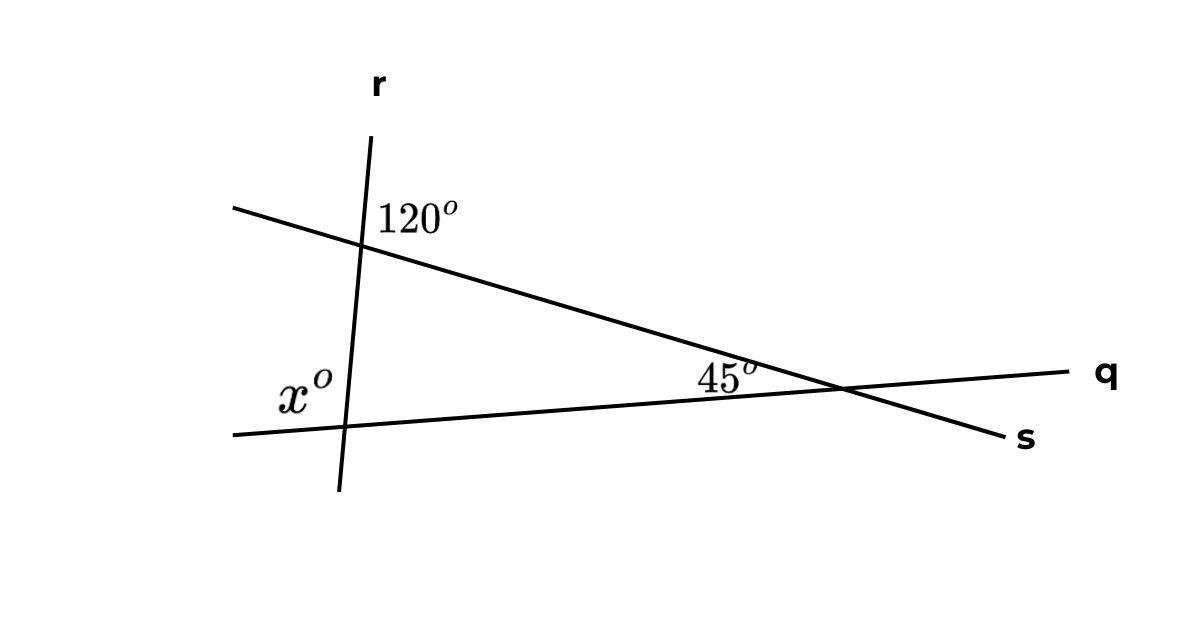
Bài 1: Intersecting lines q, r, and s are shown below. What is the value of x ?

Bài 2: In △ABC above, what is the length of AD?

Bài 3: In the diagram at left, line segment AD intersects BE and line segment AB is parallel to DE. What is the length of side CE?

Đáp án

Bài 1:

Các đường thẳng cắt nhau tạo thành một tam giác, và góc x là góc ngoài của tam giác này. Số đo của một góc ngoài của một tam giác bằng tổng số đo của hai góc trong không kề nhau của tam giác đó. Một trong hai góc này có số đo là 45 độ và góc 120 độ là góc bù → 180 - 120 = 60 độ. 

Do đó, giá trị của x là 45 + 60 = 105 độ

Bài 2:

Vì △ADB và △CBD có số đo 30-60-90 độ nên đây là hai tam giác vuông đặc biệt và chúng đều nhau Trong △ADB, cạnh AD đối diện với góc 30 độ; do đó, độ dài AD = một nửa độ dài cạnh huyền AB. Vì hai tam giác bằng nhau nên AB = BC = 16.

→ Độ dài cạnh AD = \(\dfrac{16}{2}\) = 8

Bài 3:

Gợi ý:

Theo đề bài đường AB song song đường với ED. 

Ta có góc C đối đỉnh và Giả sử BE cắt ngang hai đường song song đó, thì góc B và E là góc so le trong → △ABC và △DEC đồng dạng.

Khi hai tam giác đồng dạng, tỷ lệ giữa các cạnh tương ứng là bằng nhau

→ \(\dfrac{CE}{DE}=\dfrac{BC}{BA}\longrightarrow{}\dfrac{CE}{6.4}=\dfrac{2.4}{3.2}\)

Vậy, CE = 4.8

Đọc tiếp: Right triangle trigonometry SAT math - Tỉ số lượng giác tam giác vuông

Tổng kết

Phần thi SAT Math kéo dài 70 phút, vì vậy thí sinh cần giữ vững tâm lý và nắm chắc kiến thức để đạt kết quả cao. Hy vọng những chiến lược giải quyết dạng bài Congruence, similarity, and angle relationships đã hỗ trợ người học trong quá trình ôn tập SAT của mình. Đừng quên luyện tập các bài thực hành để củng cố lý thuyết và áp dụng hiệu quả các phương pháp vừa học.

Người học đang tìm kiếm tài liệu tự học nhằm củng cố lý thuyết và làm quen với bài toán SAT thực tế, hãy đọc thử tựa sách Think in SAT Digital Math - Reasoning and Strategies, được biên soạn bởi đội ngũ chuyên môn tại ZIM. Với mỗi dạng bài, cuốn sách sẽ cung cấp kiến thức cơ bản, các ví dụ và cách giải mẫu, cuối cùng là bài tập luyện tập kèm đáp án có giải thích chi tiết.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.