Essential vocabulary for SAT® Math - Advanced Math | Unit 1: Interpretation and Shift

Trong bài viết này, người học sẽ tìm hiểu về định nghĩa toán học của 2 từ thường gặp trong SAT Advanced Math là interpretation - thường thấy trong các bài toán non linear function, và shift - thường thấy trong các dạng bài graph transformation.

Interpretation (noun): sự diễn giải, giải nghĩa

Định nghĩa

Trong toán học, interpretation có thể được hiểu là sự gán nghĩa cho các ký hiệu, biểu thức toán học,...theo một hệ thống logic. Sự diễn giải bao gồm giải thích các ký hiệu và cách biểu thức được sử dụng trong trường hợp nào.

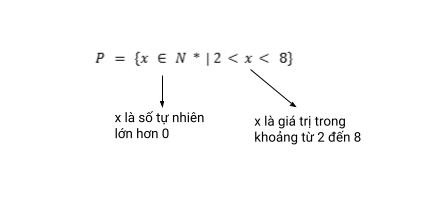
Ta có thể định nghĩa tập hợp P như sau: Tập hợp P chứa các số là số tự nhiên khác 0, các giá trị lớn hơn 2 và nhỏ hơn 8.

Ngoài ra, trong toán học, interpretation cũng dùng để giải nghĩa các đồ thị (graphical interpretation). Diễn giải ở đồ thị bao gồm việc hiểu và xử lý được thông tin từ đồ thị.

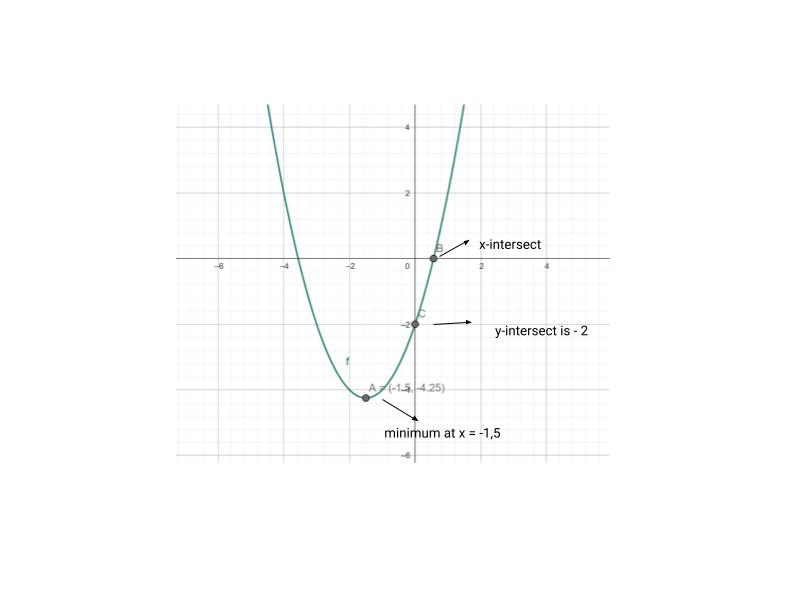
Từ tìm các giá trị cơ bản trên đồ thị như cực đại - cực tiểu, và các giao điểm của đồ thị với trục tung, trục hoành, ta có thể rút ra những kết luận cơ bản:

1. Đồ thị trên là hình parabol. Vậy đây là đồ thị của hàm số bậc hai có dạng y = ax^2 + bx + c

2. Giao điểm của trục tung là y = -2. Vậy c = -2

3. Phương trình đạt cực tiểu tại x = -b/2a = -1,5, y = -b^2/4ac = -4,25. Ta rút ra được a = 1, b = 3

4. Đồ thị hàm số bậc hai có phương trình là y = x^2 + 3x - 2

Đây là cách diễn giải đồ thị trong SAT Algebra (Đại số) và SAT Advanced Math (Toán nâng cao).

Xem thêm: Cách làm Advanced Math trong SAT Math

Shift (noun,verb): sự thay đổi, dịch chuyển

Từ đồng nghĩa: move, slide, translate

Định nghĩa

Trong mặt phẳng tọa độ, shift có nghĩa là sự thay đổi hoặc dịch chuyển đồ thị theo chiều ngang, dọc mà không làm thay đổi hình dáng ban đầu. Hay nói cách khác, sự dịch chuyển đồ thị là sự thêm hoặc bớt một số đơn vị theo trục Ox hoặc Oy.

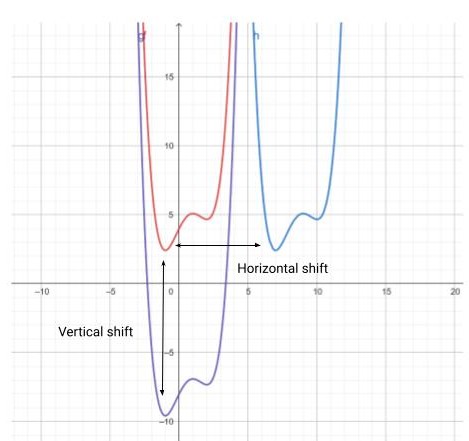
Trong hình học, sự dịch chuyển là sự thay đổi của tất cả các tọa độ theo cùng một hướng mà không làm thay đổi kích cỡ ban đầu.

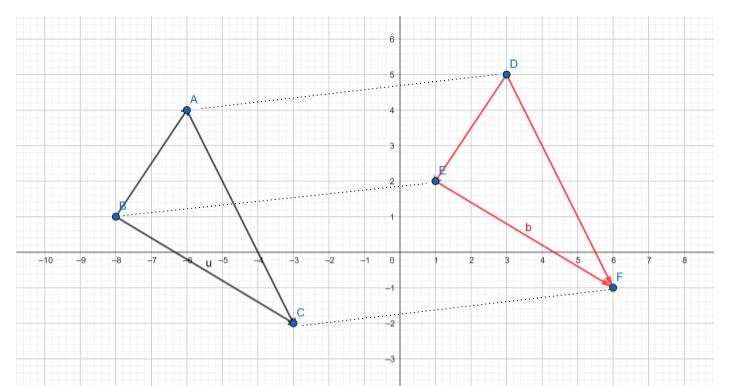
Khái niệm liên quan

1. Horizontal shift: Sự dịch đồ thị theo chiều ngang - theo trục Ox

2. Vertical shift: Sự dịch chuyển đồ thị theo chiều dọc - theo trục Oy

Kiểm tra từ vựng - interpretation

Which of the following best describes the concept of "interpretation" in mathematical logic?

A.  A method for solving equations using numerical techniques.

B. A mapping that assigns meaning to the symbols and formulas of a formal language.

C. A process of memorizing mathematical formulas.

D. A technique for proving theorems using induction.

Kiểm tra từ vựng - shift

Exercise 1: What does the term "shift" refer to in the context of graph transformations?

A. A change in the shape of the graph, such as stretching or compressing

B. A rotation of the graph around the origin

C. A movement of the graph left, right, up, or down without changing its shape

D. A reflection of the graph over an axis

Exercise 2: Fill in the blank with one of these words: shift, vertical shift, horizontal shift

1. When a function is moved up or down on a graph, this transformation is called a ________.

2. The graph of f(x)=(x−3)^2  represents a ________ of the parent function f(x)=x^2 to the right by 3 units.

3. A ________ refers to any movement of a graph without changing its shape, such as moving it left, right, up, or down.

Bài toán thực tế - interpretation

Exercise 1: 

A company is designing a noise control system for a new laundry facility. The background noise level is modeled by the equation:

y=22(0.997)^(x−60)+47

where:

• y is the estimated sound pressure level in decibels,

• x is the octave band center frequency in hertz, with x≥60

1. What might the value "47" represent in the context of the laundry room’s background noise?

2. Calculate the estimated sound pressure level y in decibels at the octave band center frequency of x=80 hertz.

Exercise 2: A drone is programmed to follow a parabolic flight path to deliver a package. The height h(t), in meters, of the drone above the ground after t seconds is modeled by the function:

h(t)= (−2).(t−6)^2+72

The drone starts at ground level, ascends, hovers briefly at its peak, and then descends to deliver the package. After reaching the ground, it immediately begins a return trip, following a different path modeled by:

r(t)=(−1.5).(t−14)^2+72

where r(t) is the height of the drone on the return trip, and t is still measured in seconds from the start of the flight.

1. What is the interpretation of 72 in this context? At which point does the drone reach its maximum height in both trips?

2. In each trip, how long can the drone stay above 50 meters?

Bài toán thực tế - shift

Exercise 1: A city monitors the number of visitors V(t) to a public park each month, modeled by the function:

V(t)=−2(t−4)^2+50

where t is the number of months since the start of the year, and V(t) is the number of visitors in thousands.

Due to a new festival, the city expects the peak number of visitors to occur 2 months later than usual, and the number of visitors to increase by 5,000 at every point in time.

1. Write the equation of the new function F(t) that models the number of visitors after the festival is introduced, applying both the horizontal and vertical shifts.

2. Calculate the number of visitors predicted by F(t) after 6 months.

Exercise 2: A company models its monthly revenue R(t), in thousands of dollars, over time t (in months) using the function:

R(t)=4t^2−3t+6

Due to a seasonal promotion, the company expects an increase in revenue of $8,000 per month for the next several months.

1. Write the equation of the new revenue function S(t) that represents the vertical shift of R(t) by 8 units upward.

2. Calculate the value of S(t) after 5 months.

3. After the 5th month, its monthly revenue sees a decrease of $5,000 per month for the next 10-month period. Write a new function D(t) to model the company's revenue during this period, and calculate the total revenue of this 10-month decreasing period.

Đáp án - interpretation

Kiểm tra từ vựng 

B. A mapping that assigns meaning to the symbols and formulas of a formal language.

Bài toán thực tế

Exercise 1:  1. minimum sound pressure level 2. y= 22.(0,997)^(20) + 47 = 67,7169dB

Exercise 2:  

1. Maximum height. Begin trip: (6;72), Return trip: (14;72)

2. 6,64s - 7,65s

Đáp án - shift

Kiểm tra từ vựng 

Exercise 1: C. A movement of the graph left, right, up, or down without changing its shape

Exercise 2: vertical shift, horizontal shift, shift

Bài toán thực tế

Exercise 1:

1. F(t)=−2(t−6)^2+55

2. 55,000

Exercise 2:

1. S(t) = 4t^2−3t+14

2. 99,000

3. t=5 is the starting point. The decrease in revenue for the next 10 months: 5.(t-5) (t>5)

After 5 months, the equation is : D(t) = S(5) - 5(t-5) = 99 - 5(t-5) = 124 - 5t (t>5)

Total revenue = D(6) + ….+ D(15) = 715 => $715,000

Trên đây là giải thích và vận dụng 2 từ interpretation và shift trong các bài toán thực tế. Người học nên luyện tập và ứng dụng những từ trên để có thể làm tốt trong các bài thi SAT Math.

Để đạt kết quả cao trong kỳ thi SAT, việc nắm vững chiến lược và phương pháp giải các dạng toán là yếu tố then chốt. Sách Think in SAT Digital Math - Reasoning and Strategies cung cấp cho thí sinh cái nhìn tổng quan về các dạng toán trong kỳ thi, cùng hướng tư duy hiệu quả để giải quyết từng dạng bài. Mỗi chủ đề được trình bày với kiến thức cơ bản, ví dụ minh họa, cách giải mẫu và bài tập luyện tập kèm đáp án chi tiết.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.