Phương pháp giải các dạng bài trong SAT Math (P2)

Xác suất thống kê (Problem Solving and Data Analysis) là một trong bố chủ đề của phần thi Toán của bài thi SAT Math. Ở phần trước, bạn đọc đã được giới thiệu về toàn bộ chủ đề Đại số căn bản (Heart of Algebra) và dạng bài đầu tiên của Xác suất thống kê. Bài viết này sẽ giới thiệu tới bạn đọc chi tiết về các dạng bài còn lại của chủ đề Xác suất thống kê và các công cụ cũng như chiến thuật để xử lí các bài tập đó.

Xác suất thống kê (Problem Solving and Data Analysis) trong SAT Math

Dạng 2: Bài toán biểu diễn mối quan hệ giữa biểu đồ phân tán, đồ thị, bảng với phương trình.

(Các bài tập của dạng bài này tập trung vào mối quan hệ giữa hai đối tượng với nhau)

Biểu đồ phân tán

Trong thực tế, các thí nghiệm thường có số liệu không chính xác tuyệt đối do các yếu tố ngoại cảnh. Điều này dẫn tới việc khi xây dựng các mô hình biểu diễn số liệu thì các các điểm biểu diễn sẽ phân tán đi thành một vùng chứ không thành một đường đồ thị nhất định. Do đó, bài toán SAT Math này yêu cầu thí sinh lý tưởng hoá các số liệu để xây dựng một biểu thức và đồ thị đơn giản giúp thuận lợi cho việc tính toán.

Các dạng bài tập SAT Math thí sinh có thể gặp với biểu đồ phân tán: tìm đường biểu diễn (the line best fit), tính toán dựa trên đường biểu diễn, tính số các điểm có giá trị lớn hơn/nhỏ hơn so với đường phỏng đoán.

Ví dụ

Câu hỏi dưới đây là điển hình cho một bài tập về biểu đồ phân tán

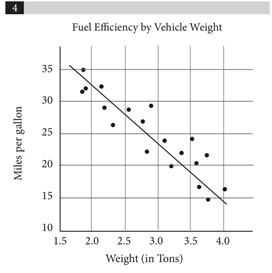
(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

Đối với biểu đồ phân tán, để tìm được đường biểu diễn, hãy vẽ đường gần nhiều điểm nhất có thể. Đối với các bài tập trong SAT thì đường biểu diễn đa phần là các đường thẳng, do đó đường được chọn cần phải đại diện cho dáng điệu của tập hợp các điểm trên biểu đồ.

Đối với các dạng bài SAT Math yêu cầu đếm số giá trị mà có giá trị thực thấp hơn hoặc lớn hơn giá trị phỏng đoán (giá trị phỏng đoán là điểm nằm trên đường biểu diễn), giá trị này tương đương với các điểm nằm ở dưới hoặc trên đường biểu diễn.

Giải quyết ví dụ

Bài toán này được giải quyết bằng cách sử dụng đồ thị (the line best fit). Dựa vào đường biểu diễn, đề bài yêu cầu tìm số dặm đi được với mỗi gallon của phương tiện nặng 3 tấn. Dóng từ trục hoành (trục khối lượng), số dặm một bình tương ứng với phương tiện 3 tấn là khoảng 24 dặm. (Dóng thẳng đứng) Vậy đáp án đúng là B.

Đồ thị

Yêu cầu

Dạng bài SAT Math này yêu cầu thí sinh hiểu được mối liên hệ giữa tình huống thực tế và đồ thị biểu diễn chúng. Đa phần các đồ thị trong phần bài tập này đều là hàm tuyến tính vậy nên thí sinh cần có nền tảng ở phần Hàm số tuyến tính và phương trình bậc nhất.

Các dạng đồ thị thường gặp: Đồ thị vận tốc – thời gian, đồ thị quãng đường – thời gian, số lượng sản phẩm – thời gian,…

Ví dụ

Cùng xem xét câu hỏi dưới đây

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

Đối với dạng bài tập này, thí sinh cần chú ý những điều sau:

• Các đối tượng được biểu trên đồ thị được biểu diễn với số lượng và đơn vị nào. Chẳng hạn sẽ có những đồ thị biểu diễn số dân với đơn vị là triệu người. Điều này là cần thiết bởi kết quả khi tính toán có thể khác với yêu cầu của đề bài bởi sự khác nhau về đơn vị.

• Xác định xem giữa các đối tượng có mối liên hệ như thế nào (về độ thay đổi). Ví dụ: Quãng đường = vận tốc x thời gian; Số dân = hệ số gia tăng theo năm x số năm;… Các câu hỏi của bài tập này cũng thường hỏi về các đại lượng thứ ba đặc trưng cho mối quan hệ giữa đại lượng trong đồ thị.

Giải quyết ví dụ

Đồ thị biểu diễn quãng đường theo thời gian. Đề bài yêu cầu tính tốc độ của Glenn trong khoảng thời gian chạy bộ. Để giải quyết câu hỏi này, thí sinh cần nhớ công thức tính tốc độ bằng tổng quãng đường đi được chia cho tổng thời gian. Hay nói cách khác vận tốc (trong trường hợp này vận tốc và tốc độ có thể coi là một) chính là độ thay đổi của quãng đường theo thời gian.

Đường đồ thị của Glen là phần nét đứt, như vậy ta có thể xác định được tổng quãng đường và thời gian bằng điểm cuối của đồ thị này. Đó là điểm (15; 3000). Tức là sau 15p thì Glen đi được là 3000m. Để thuận lợi, đổi 15p thành 15 x 60 = 900s (vì đề bài hỏi vận tốc dưới đơn  vị m/s).  Vậy tốc độ trung bình của Glen là .

Bảng

Yêu cầu

Phần bảng biểu nằm trong SAT Math chỉ tập trung vào mối quan hệ giữa hai đối tượng. Thí sinh được cung cấp một bảng và có nhiệm vụ xây dựng hàm biểu diễn cho hai đối tượng đó.

Ví dụ

Cùng xem xét ví dụ đơn giản dưới đây. (Ngoài ra sẽ có các bài được thực tế hoá bằng cách sử dụng các đại lượng trong đời sống.)

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

Có hai cách để giải quyết bài toán này

• C1: Sử dụng công thức của phần Hàm số tuyến tính để giải. Từ công thức đường thẳng đi qua hai điểm, ta có thể xác định được hệ số góc và sau đó là hệ số tự do của phương trình.

• C2: Thử từng đáp án. Thí sinh có thể thử các điểm vào từng đáp án, sau đó loại trừ dần đến đáp án đúng nhất.

Việc lựa chọn phương án giải nào tùy thuộc vào từng bài toán. Đối với các bài toán có số liệu phức tạp hoặc lớn, thí sinh tránh sử dụng phương án thử và loại trừ bởi tính toán có thể nhầm lẫn và tốn thời gian.

Tuy nhiên khi các bài toán có logic phức tạp, mối quan hệ giữa hai đối tượng không rõ ràng khiến cho việc xây dựng mô hình trở nên khó hơn, thí sinh có thể sử dụng phương án loại trừ để tìm ra đáp án.

Giải quyết ví dụ

Đối với bài toán SAT Math này, cả hai cách làm đều có thể áp dụng được, tuy nhiên cách 1 có thể tìm ra kết quả nhanh hơn.

Như đề bài đã nêu, các điểm trên đều thuộc một đường thẳng. Do đó, từ công thức đường thẳng đi qua hai điểm, ta có thể xác định được hệ số góc và sau đó là hệ số tự do của phương trình. Đầu tiên là công thức hệ số góc, chọn điểm (1,1) và (2,4), có: k = (4-1)/(2-1)=3

Phương án duy nhất có hệ số góc bằng 3 là phương án B. Vậy phương án đúng là B.

Biểu đồ cột

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Giải quyết ví dụ

Bài tập SAT Math trên yêu cầu thí sinh tìm đại lượng và đơn vị phù hợp cho trục hoành của biểu đồ cột. Bài tập này yêu cầu kỹ năng định tính tốt từ thí sinh. Đầu tiên, có thể thấy rằng tổng dân số của 6 nước là ≈ 3,49 tỷ người. Do đó, nếu đơn vị của trục hoành là tỷ người (billions of people) tức là Trung Quốc sẽ có đến 1200 tỷ người, do đó đáp án này là vô lý. Nếu đơn vị là nghìn người (thousands of people), số dân của mỗi nước mới dừng ở mức vài triệu người (rất nhỏ) so với tổng số. Tương tự đơn vị là người cũng bị loại. Do đó đáp án đúng là B) in millions of people.

Dạng 3: Biểu đồ phân bố

(Tables, bar graphs, histograms, dot plots, box plots, line graphs, or other displays)

Yêu cầu chung

Khác với các biểu đồ và đồ thị ở phần trước, các bài tập trong phần này tập trung vào sự phân bố số liệu. Về cơ bản, các yêu cầu là tương đồng với nhau, điều khác biệt là cách sắp xếp bố trí dữ liệu đặc trưng của mỗi loại biểu đồ. Vậy nên phần này bài viết sẽ cung cấp các thông tin chung và các mẹo nhỏ cho từng dạng.

Kiến thức cần nhớ trong SAT Math

Trung bình (Mean)

Có hai loại trung bình trong toán học là trung bình cộng (arithmetic mean) và trung bình nhân (geometric mean). Các bài toán xác suất trong SAT thường tập trung vào trung bình cộng, mean được hiểu là trung bình cộng ở phần lớn các bài.

Trung bình cộng được tính bằng cách lấy tổng các số hạng chia cho số số hạng: 

Mean = (a1 + a2 +… an)/n

Số trung vị (Median)

Trong một tập hợp các số, số trung vị là số hạng đứng ở giữa khi ta sắp xếp các số hạng thành 1 dãy có giá trị từ bé đến lớn. Ví dụ: Dãy 1, 2, 5, 7, 9, 10, 11. thì số 7 là số trung vị.

Đối với dãy có số chẵn các số hạng thì số trung vị được tính bằng trung bình cộng hai số ở giữa. Ví dụ: 1, 2, 5, 7. Thì số trung vị là (2 + 5)/2 = 3,5.

Kể cả khi các số hạng trùng lặp, ta vẫn sắp xếp theo thứ tự như bình thường. Ví dụ:

• 1, 1, 2, 4, 5 ,5, 7. Số trung vị vẫn là 4.

• 1, 2, 3, 3, 5. Số trung vị là 3.

• 1, 2, 3, 3, 5, 5, 7, 8. Số trung vị là (3 + 5)/2 = 4.

Số Mode

Trong một tập hợp, số Mode là số hạng xuất hiện với tần suất nhiều nhất trong cả tập.

Ví dụ:

• Cho tập 2, 2, 3, 3, 5, 5, 5, 6, 6, 6, 6, 7.

• Số 2 xuất hiện 2 lần, 3 xuất hiện 2 lần, 5 xuất hiện 3 lần, 6 xuất hiện 4 lần, và 7 xuất hiện 1 lần. Vậy số Mode là 6.

Lưu ý:

• Khi cả hai số cùng xuất hiện 1 tần suất và là nhiều nhất trong tập, cả 2 số đều là Mode.

• Số Mode là số hạng xuất hiện nhiều nhất chứ không phải là tần suất xuất hiện của số hạng.

Range

Miền giá trị (range) được xác định là chênh lệch giá trị giữa số hạng lớn nhất và giá trị bé nhất trong tập.

Standard Deviation

Độ lệch chuẩn (Standard Deviation) là đại lượng dùng để xác định mức độ phân tán của số liệu. Độ lệch chuẩn được xác định bằng căn bậc hai của phương sai. Tuy nhiên bài thi SAT không yêu cầu thí sinh tính toán đại lượng này mà chỉ so sánh định tính với nhau.

Dạng Bảng

Ví dụ

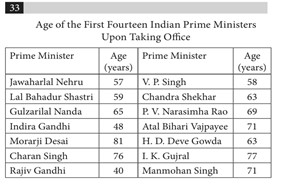
(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Giải quyết ví dụ

Bài toán trên hỏi tuổi trung bình của 14 bộ trưởng Ấn Độ. Để xác định được tuổi trung bình, theo công thức, lấy tổng số tuổi của 14 vị rồi sau đó chia cho 14, có:

(Đề bài yêu cầu làm tròn đến số thập phân đầu tiên — the nearest tenth)

Dạng biểu đồ cột

Ví dụ

A police office recorded the travel speeds, in miles per hour, of traffic on a major arterial road. The histogram to the left shows the number of vehicles driving at each speed. Which statement best compares the mean and the median of the data?

(Nguồn Khan Academy)

Giải quyết ví dụ

Đề bài yêu cầu thí sinh so sánh giữa số trung bình cộng và số trung vị, vậy nhiệm vụ đầu tiên là xác định hai số đó. Tuy nhiên, để ý một chút thì đáp án không yêu cầu một số liệu cụ thể, và đặc biệt đáp án D còn có từ ‘approximately’. Vậy trong bài này thí sinh có thể sử dụng kiểu ước chừng và định tính để giải quyết.

Về trung bình cộng, việc các số từ 57-62 có tần suất xuất hiện lớn nhất kèm với tính đối xứng của đồ thị cho thấy rằng trung bình cộng của các số hạng sẽ nằm vào vùng ở giữa (57 – 62). Điều này có thể được suy ra từ các nhận xét sau:

• Khi ta thêm một số mới vào một tập cho trước, thì trung bình cộng của tập mới sẽ tiến dần về giá trị của số mới thêm vào.

Ví dụ: Tập gồm {1, 1, 2, 3, 4, 5, 6, 7}. Có trung bình cộng là 3,625. Khi cho thêm một số 4 vào, trung bình cộng của dãy mới là: 3,667. Tiếp tục thêm một số 4 nữa, trung bình cộng của dãy là 3,7. Càng thêm nhiều số 4 thì giá trị trung bình cộng của tập càng gần 4.

Do đó, nếu trong một tập mà tần suất xuất hiện của một số hạng nào càng lớn thì giá trị trung bình cộng của tập càng gần với số đó (Mode).

Đối với số trung vị, thí sinh cần sắp xếp các số hạng theo thứ tự từ nhỏ đến lớn. Cách để xác định số trung vị với tập có số lượng lớn như sau:

• Xác định số lượng số hạng và tìm vị trí số trung vị bằng cách lấy số lượng số hạng chia đôi.

• Tìm số trung vị tương ứng với số thứ tự.

Như trên biểu đồ ví dụ, do các số hạng được phân bố đối xứng, hơn nữa các số nằm trong khoảng 57-62 có tần suất xuất hiện nhiều nhất, thí sinh có thể kết luận rằng khoảng này chính là khoảng chứa số trung vị.

Biểu đồ chấm (Dot plot)

Ví dụ

(Nguồn Khan Academy)

Lưu ý

Đây là một biểu đồ khá lạ lẫm với học sinh Việt Nam vì hiếm khi được giới thiệu trong chương trình học phổ thông. Tuy nhiên biểu đồ này khá trực quan và thí sinh có thể làm quen nhanh chóng.

Mỗi chấm sẽ tương ứng với một đối tượng. Và phần trục (có thể là ngang hoặc dọc) là biểu diễn cho giá trị tương đương với mỗi đối tượng đó trong cùng một tiêu chí so sánh.

Đối với bài ví dụ:

• Mỗi chấm trên biểu đồ tương ứng với một quốc gia.

• Phần trục hoành tương ứng độ dài của đường bờ biển của quốc gia đó.

Đặc điểm của biểu đồ này là thể hiện sự phân bố của giá trị (độ dài đường bờ biển) chứ không phải các đối tượng (thông tin chi tiết từng quốc gia tương ứng).

Giải quyết ví dụ

Để tính trung bình cộng đường bờ biển các quốc gia Nam Mỹ trong bảng, thí sinh cần tìm được tổng độ dài bờ biển, sau đó lấy tổng này chia cho số quốc gia. Bảng có 15 chấm, tức có 15 quốc gia. Để tính tổng, thí sinh cộng độ dài tương ứng của từng chấm lại với nhau. Cách tính nhanh hơn là lấy độ dài nhân số chấm tương ứng rồi cộng lại với nhau. Kết quả cuối cùng cho ra tổng độ dài là: 30 (nghìn km). (Chú ý đơn vị). Sau đó trung bình cộng độ dài đường bờ biển là: 30/15 = 2 (nghìn km). Đề bài yêu cầu để đáp án có đơn vị là nghìn km, do đó thí sinh cần điền đáp án là 2.

Biểu đồ hộp (Box Spot)

Ví dụ

(Nguồn Khan Academy)

Lưu ý

Đây cũng là một biểu đồ khá lạ lẫm với học sinh Việt Nam vì hiếm khi được giới thiệu trong chương trình học phổ thông. Và biểu đồ SAT Math này có thể khó tiếp cận hơn so với biểu đồ chấm. Đây là cấu tạo cơ bản của biểu đồ:

Phần hộp:

Gạch ở giữa hộp (màu đỏ) chính là biểu diễn cho số trung vị. Khi dóng thẳng gạch này xuống trục sẽ xác định được giá trị số trung vị.

Gạch đầu bên trái của hộp là điểm tứ phân vị nhỏ (lower quartile), gạch đầu bên phải là điểm tứ phân vị lớn (upper quartile). Thứ tự trái phải, trên dưới phụ thuộc vào trục biểu diễn đi kèm với hộp.

• Tứ phân vị nhỏ được hiểu là điểm chính giữa của số trung vị và giá trị nhỏ nhất trong tập.

• Tứ phân vị lớn được hiểu là điểm chính giữa của số trung vị và giá trị lớn nhất trong tập.

Phần đoạn thẳng ở hai đầu hộp: Hai dấu chấm ở hai đầu mút của đoạn thẳng biểu diễn giá trị nhỏ nhất và lớn nhất trong tập hợp. Vị trí (trái phải, trên dưới) phụ thuộc vào trục biểu diễn.

Phần trục biểu diễn giá trị các đối tượng.

Giải quyết ví dụ

Bài tập SAT Math yêu cầu tính miền giá trị của tập. Dựa vào hai đầu mút, thí sinh dóng xuống trục giá trị có thể xác định được giá trị nhỏ nhất là khoảng 39 còn giá trị lớn nhất là khoảng 102. Như vậy miền giá trị ≈ 102 – 39 = 63. Chọn đáp án gần nhất là C) 62.

Các câu hỏi khác (Other questions)

Ngoài việc xử lí các bài toán về bảng và biểu đồ, bài thi SAT còn yêu cầu thí sinh giải quyết các câu hỏi liên quan đến phương pháp đo lường và xử lí số liệu. Dưới đây là một số dạng câu hỏi điển hình cho các câu hỏi này.

Dạng câu hỏi giải thích về kết quả số liệu dựa trên tình huống

Ví dụ

Cùng xem xét câu hỏi dưới đây

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

B1: Đọc kỹ đề bài và xác định đối tượng được nhắc đến. Đánh dấu các đại lượng và kết quả nghiên cứu thu được.

B2: Phân tích các kết quả thu được và suy luận ra cách tính toán các đại lượng như trung bình cộng, trung vị, mode, độ lệch chuẩn,… dựa vào cách tính toán các đại lượng được cung cấp trung phần kiến thức cần nhớ ở trên. Các câu hỏi sẽ hỏi về các đại lượng này và so sánh các đại lượng này với nhau trong cùng một tập hợp các kết quả của nghiên cứu. Do đó thí sinh cần nắm chắc nội dung này.

B3: Loại trừ các phương án bất hợp lí hoặc kém hợp lí hơn.

Giải quyết ví dụ

Đề bài hỏi rằng đâu là phương án giải thích hợp lý cho việc trung vị thu nhập các hộ gia đình của Mỹ thấp hơn so với trung bình cộng thu nhập các hộ gia đình.

Nhắc lại kiến thức cần nhớ. Với trung vị, đại lượng này có đặc điểm là không phụ thuộc vào miền giá trị của tập, tức là dù các phần tách biệt (lớn nhất nhỏ nhất) có lớn đến đâu thì trung vị vẫn có thể không đổi, miễn là thứ tự lớn bé không đổi. Trong khi đó, với trung bình cộng, như đã lưu ý ở phần trước, khi thêm một số hạng mới vào tập thì trung bình cộng của tập mới sẽ có giá trị tiến dần về phía của số hạng đó.

Ở trường hợp này, số trung bình cộng lớn hơn nhiều so với số trung vị, vậy sự khác biệt khả năng cao sẽ đến từ việc có những số hạng nào đó lớn tách biệt so với phần còn lại, kéo cho giá trị trung bình tiến dần về phía nó, nhưng lại ít ảnh hưởng đến số trung vị. So với các phương án còn lại, đây là phương án hợp lí hơn cả vì tập trung đúng vào sự khác nhau cốt lõi trong đặc điểm của trung bình cộng và trung vị. Vậy phương án đúng là B.

Dạng câu hỏi đưa ra kết luận từ số liệu

Ví dụ

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

B1: Đọc kỹ đề bài và đánh dấu đối tượng nghiên cứu, phương pháp lấy và xử số liệu.

B2: Xác định mức độ chắc chắn của kết quả nghiên cứu. Dựa vào các tiêu chí sau của mẫu nghiên cứu: số lượng, chủng loại, điều kiện,… Các tiêu chí được phủ càng rộng thì mức độ chắc chắn càng cao và độ bao phủ càng rộng.

B3: Phân tích các đáp án, đánh dấu các từ chỉ mức độ (tương đối, tuyệt đối) và chọn đáp án phù hợp với phân tích ở trên.

Giải quyết ví dụ

Đề bài hỏi rằng đâu là kết luận hợp lí nhất từ nghiên cứu được nêu trong bài SAT Math. Dựa vào độ lớn của mẫu thử là 400 phương tiện chạy xăng ngẫu nhiên, có thể thấy rằng mẫu thử này còn khá nhỏ về số lượng, ngoài ra cũng không biết chính xác số lượng của mỗi loại phương tiện. Do đó không thể kết luận một cách tuyệt đối. Để ý vào các đáp án, phương án A, B, và C đều khẳng định tương đối chắc chắn về tiềm năng của loại dầu E. Điều này là thiếu cơ sở vì lí do phân tích ở trên. Phương án hợp lí nhất là D vì kết luận được đưa ra ở một mức độ chắc chắn phù hợp.

Dạng 4: Câu hỏi về phương pháp xử lí số liệu

Ví dụ

(Nguồn Cracking SAT 2020 Practice Tests — The Princeton Review)

Chiến thuật

Đối với các bài tập SAT Math dạng này, phương pháp loại trừ là một phương án tối ưu vì các bài tập này yêu cầu khả năng định tính cao của thí sinh. Do đó, hãy sử dụng suy luận và các nội dung cung cấp trung phần Kiến thức cần nhớ về các thao tác xử lí số liệu để xử lí các bài tập này.

Giải quyết ví dụ

Loại trừ lần lượt các đáp án. Đề bài hỏi đâu là yếu tố khiến cho cuộc thăm dò ý kiến thiếu chính xác (hay ít độ tin cậy) nhất.

Phương án A nói đó là phương thức phân phát phiếu thăm dò. Tuy nhiên đề bài nói rằng các phiếu thăm dò đều được phát ngẫu nhiên, do đó không có sự sai lệch hay thiên vị về một đối tượng nhất định nào. Do đó phương án này khả năng cao không gây ra sai lệch.

Phương án B đề cập đến thời gian xin ý kiến. Các đối tượng được thăm dò đã sử dụng dịch vụ từ một năm trước, điều này có thể khiến cho các ý kiến không còn chính xác. (Các đối tượng có thể nhầm lẫn các lần sử dụng dịch vụ với nhau, hoặc thậm chí không nhớ rõ). Đây có thể là phương án cần tìm.

Phương án C và D đều đề cập đến số lượng. Con số 550 người được lựa chọn ngẫu nhiên là một số lượng tương đối ổn và không có tính thiên vị (biased). Ngoài ra số lượng trả lời cũng lớn (415 người, tương đương 75%), do đó đây không phải vấn đề lớn.

Từ các phân tích trên, phương án hợp lý nhất là phương án B.

Đọc thêm: Luyện thi SAT – Những điều cơ bản cần biết

Tổng kết

Như vậy, nhìn chung phần kiến thức về SAT Math còn khá mới lạ với nhiều học sinh Việt Nam vì chương trình phổ thông chưa được cập nhật nhiều các nội dung này. Tuy nhiên, với các kiến thức nền toán học sẵn có, thí sinh có thể nhanh chóng làm quen và xử lí các bài tập này. Đôi khi các câu hỏi của dạng bài trong SAT Math có thể khiến thí sinh nhanh nản chí vì đề bài khá dài và số lượng dữ kiện lớn, phức tạp. Có một số câu hỏi thuộc phần “Các câu hỏi khác” có thể là những câu hỏi khó nhất trong đề bởi tính không rõ ràng và yêu cầu định tính cao của chúng. Dù vậy, tác giả hy vọng rằng bài viết này có thể giúp bạn đọc có một cái nhìn đơn giản và trực quan hơn với những vấn đề đó, từ đó tìm ra phương pháp làm bài tối ưu cho mình.

Đọc thêm: Những điều cần biết về Math Test SAT và các thuật ngữ Toán Đại Số

Phạm Tuấn Minh