Áp dụng lý luận logic vào câu hỏi suy diễn trong TOEFL – Phần 1

Khi người đọc có thể sử dụng những thông tin đưa ra bởi tác giả để trả lời một câu hỏi đọc hiểu (Comprehension question), điều được kiểm tra ở đây chính là sự đọc hiểu có căn cứ (Factual comprehension) của người đó, tức hoàn toàn dựa trên những câu từ xuất hiện trong bài đọc. Tuy nhiên, không phải lúc nào thông tin cần thiết cho việc trả lời câu hỏi cũng sẽ được trình bày và định rõ ở trong bài đọc. Trong những trường hợp này, người đọc được yêu cầu phải sử dụng lý luận logic của mình để tự suy ra câu trả lời. Sự đọc hiểu này đôi khi còn được gọi là sự đọc hiểu suy diễn (Inferential comprehension).

Inference questions

Những câu hỏi suy diễn yêu cầu người đọc lập luận và giả định một cách logic từ việc kết nối và suy luận từ những thông tin có sẵn trong trong đoạn văn để đưa ra một kết luận mới. Nói cách khác, một câu hỏi suy luận yêu cầu người đọc hiểu được thông tin đang được đưa ra một cách gián tiếp hoặc là được ẩn ý, thay vì được nêu ra trực tiếp trong đoạn văn. Các câu hỏi dạng này thường sẽ có thông điệp chứa những từ như là “imply”, “suggest”, hoặc là “infer”.

Logical Reasoning

Lập luận logic là một quy trình tư duy mà cho phép người tư duy tạo nên những cách hình dung mới dựa trên những kiến thức, thông tin sẵn có. Nó xoay quanh việc xử lý nhận thức nhằm tìm ra giải pháp cho các vấn đề bằng cách đưa ra kết luận dựa trên các quy tắc logic hoặc các thủ pháp hợp lý. Khi lập luận logic, người tư duy cần cố gắng phải vượt ra khỏi ngoài thông tin được cung cấp để đưa ra một cách hình dung, nhìn nhận vấn đề hợp lý.

Formal logic

Logic hình thức (formal logic) cung cấp một hệ thống mang tính công thức máy móc cho việc suy diễn. Hê thống này bao gồm một tập hợp nhiều quy tắc và ký hiệu; lập luận được thực hiện trong hệ thống này sẽ dẫn tới những kết quả hợp lý miễn là người lập luận bám sát theo theo những quy tắc. Việc lập luận này thường được gọi là lập luận hình thức (formal reasoning) và thường có đặc trưng là các quy tắc logic và quy tắc toán học, với những tiền đề cố định và không thay đổi (giống như một hằng số).

Khi một người lập luận logic một cách hình thức, họ đang tuân theo một hệ thống các quy tắc mà chỉ rõ ra việc họ phải rút ra kết luận như thế nào.

Logic hình thức (formal logic) sinh ra một loại lập luận mà được sử dụng nhiều trong ngữ cảnh học thuật gọi là lý luận diễn dịch (Deductive reasoning). Về mặt logic, lý luận diễn dịch áp dụng một quy trình suy luận được gọi là Tạm đoạn luận logic (Logical Syllogism).

Mọi tam đoạn luận logic đều phải mang 2 tính chất sau:

1. Tính xác thực: Các tiền đề phải mang tính xác thực.

2. Tính hợp lý: Một kết luận có thể rút ra được từ các tiền đề để trả lời câu hỏi.

Ví dụ sau đây về tam đoạn luận logic có thể sẽ rất quen thuộc với người đọc.

Tiền đề chính: All men (A) are mortal (B)                                A=B

Tiền đề phụ: Socrates (C) is a man (A)                                    C=A

Kết luận: Therefore, Socrates (C) is mortal (B)                        C=B

Và đúng thật như vậy, Socrates đã chết và điều này nghĩa rằng kết luận được rút ra là chính xác.

Xem thêm: Tư duy logic là gì – Các kiểu lập luận theo tư duy phi logic phổ biến

Về mặt logic, một kết luận xác thực sẽ theo sau những tiền đề xác thực. Kết luận này, chỉ mình nó, không phải là lập luận – mà là một phần của lập luận. Nó là một kết quả logic từ những suy luận được đúc kết từ những tiền đề. Sự kết hợp của tất cả những yếu tố này, trong một toàn thể, là một lập luận.

Ngoài hệ thống lập luận tam đoạn luận như trên, có một quy tắc liên quan đến toán học hay được áp dụng ở trong lập luận logic hình thức là phương pháp sơ đồ Euler – được định nghĩa ngắn gọn là một biểu đồ minh hoạ các mối quan hệ giữa nhiều nhóm đối tượng; sơ đồ Euler thông thường được vẽ sử dụng các hình tròn (hoặc hình cầu) mà có thể trùng lặp với nhau.

Xét ví dụ sau:

Tiền đề 1: Mọi A là B

Tiền đề 2: Vài B là C

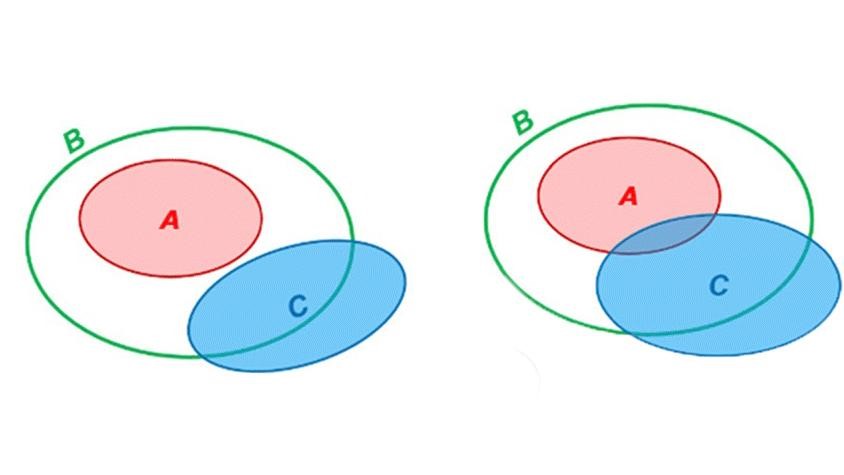
Khi sử dụng sơ đồ Euler, ta có thể hình dung mối quan hệ giữa A,B và C như sau:

Như vậy, ngoài kết luận thông thường hay được suy ra đó là “Vài A là C” (hình phải), thì còn có một kết luận khả thi nữa là A và C không có liên quan gì với nhau (hình dưới).

Informal Logic

Logic phi hình thức (informal logic) là một thuật ngữ rộng cho bất kỳ phương pháp phân tích và đánh giá lập luận nào được sử dụng trong cuộc sống hàng ngày. Logic phi hình thức thường được coi là một giải pháp thay thế cho logic hình thức hoặc toán học. Còn được gọi là logic phi chính thức hoặc tư duy phản biện. 

Lý luận phi hình thức (Informal reasoning) là một sự lý luận liên quan đến cách dùng ngôn ngữ hằng ngày để hình thành một lập luận mà yêu cầu việc xem xét một cách phản biện các tiền đề (premises), xử lí và chuyển đổi thông tin. Ngoài ra, người giải quyết vấn đề còn phải biết tự tìm những thông tin tương tự, hoặc  để ẩn ý giữa những thông tin sẵn có. Logic phi hình thức khác logic hình thức ở chỗ nó nhấn mạnh những yếu tố, nội dung liên quan đến cách dùng ngôn ngữ của lập luận.

Trong một lập luận phi hình thức (informal reasoning), logic hình thức chỉ đóng một vai trò phụ là cung cấp một cấu trúc lập luận (gồm những tiền đề và kết luận), còn phần trọng tâm của lập luận vẫn phụ thuộc vào ý nghĩa và nội dung; cụ thể hơn bao gồm những yếu tố như nghĩa bóng, nghĩa đen và các tầng nghĩa của cùng một từ, v.v.

Xem thêm: Tiền đề phụ thuộc và cách ứng dụng trong xây dựng lập luận

Khi lập luận một cách phi hình thức, người tư duy phải rút ra những suy diễn từ những tiền đề được coi là không chắc chắn; những tiền đề này có thể mang tính mở, chung chung, hoặc chưa rõ ràng.

Xét ví dụ sau:

“Một điều phối viên của Hiệp hội Nhân đạo ủng hộ án tù, cho rằng các hình phạt nhẹ thường được áp dụng cho những tội nhẹ không đủ sức răn đe trong các trường hợp này.”

Tiền đề: Các hình phạt nhỏ thường được áp dụng cho tội nhẹ không đủ sức răn đe trong trường hợp này.

Tiền đề ngầm: Hình phạt cho tội phạm cần có tác dụng răn đe.

Kết luận: Mức án tù là phù hợp.

Tổng kết

Trong phần tiếp theo của “Áp dụng lý luận logic vào câu hỏi suy diễn trong TOEFL“, tác giả sẽ chỉ ra vai trò của lý luận logic trong đọc hiểu học thuật, cũng như hướng dẫn người đọc cách ứng dụng lý luận logic vào dạng bài này.

Nguyễn Văn Đăng Duy