Parallel lines là gì? Tính chất, các định lí, cách giải và bài tập

Trong hình học, khái niệm đường thẳng song song (parallel lines) là cơ sở để xây dựng nhiều định lý, chứng minh, cũng như giải quyết các bài toán liên quan đến góc, khoảng cách và hình phẳng. Trong kỳ thi SAT®, kiến thức về đường thẳng song song xuất hiện thường xuyên, đặc biệt trong các câu hỏi về tam giác, tứ giác và tọa độ.

Bài viết giới thiệu khái niệm, ký hiệu, tính chất và cách giải bài parallel lines, từ đó giúp người học có nền tảng vững chắc để vận dụng chính xác trong học tập và ôn luyện.

Khái niệm đường thẳng song song (parallel lines) và tính chất cơ bản

Định nghĩa, ký hiệu và đặc điểm nhận biết parallel lines

Trong hình học Euclid, hai đường thẳng được gọi là song song (parallel lines) nếu chúng cùng nằm trong một mặt phẳng nhưng không bao giờ cắt nhau.

Nếu hai đường thẳng a và b song song, chúng được kí hiệu là a||b.

Dấu hiệu đặc trưng của hai đường thẳng song song:

• không có điểm chung;

• khoảng cách vuông góc từ một điểm bất kỳ trên đường thẳng này đến đường kia luôn bằng nhau, nghĩa là chúng cách đều nhau trên toàn bộ chiều dài.

Tính chất: khoảng cách giữa hai đường song song (parallel lines) luôn không đổi

Một tính chất cơ bản của hai đường thẳng song song là khoảng cách giữa chúng luôn không đổi. Khoảng cách này được xác định bởi đoạn thẳng vuông góc hạ từ một điểm trên đường thẳng này đến đường thẳng kia. Dù chọn điểm nào, kết quả luôn không thay đổi.

Đây là nền tảng để chứng minh các định lý trong hình học, cũng như để giải quyết các bài toán tọa độ, ví dụ như tính khoảng cách giữa hai đường thẳng song song.

Phân biệt parallel lines với đường vuông góc và đường cắt nhau

Trong hình học phẳng, ngoài quan hệ song song, các đường thẳng còn có thể vuông góc hoặc cắt nhau. Việc phân biệt đúng các quan hệ này có ý nghĩa quan trọng trong chứng minh và giải toán.

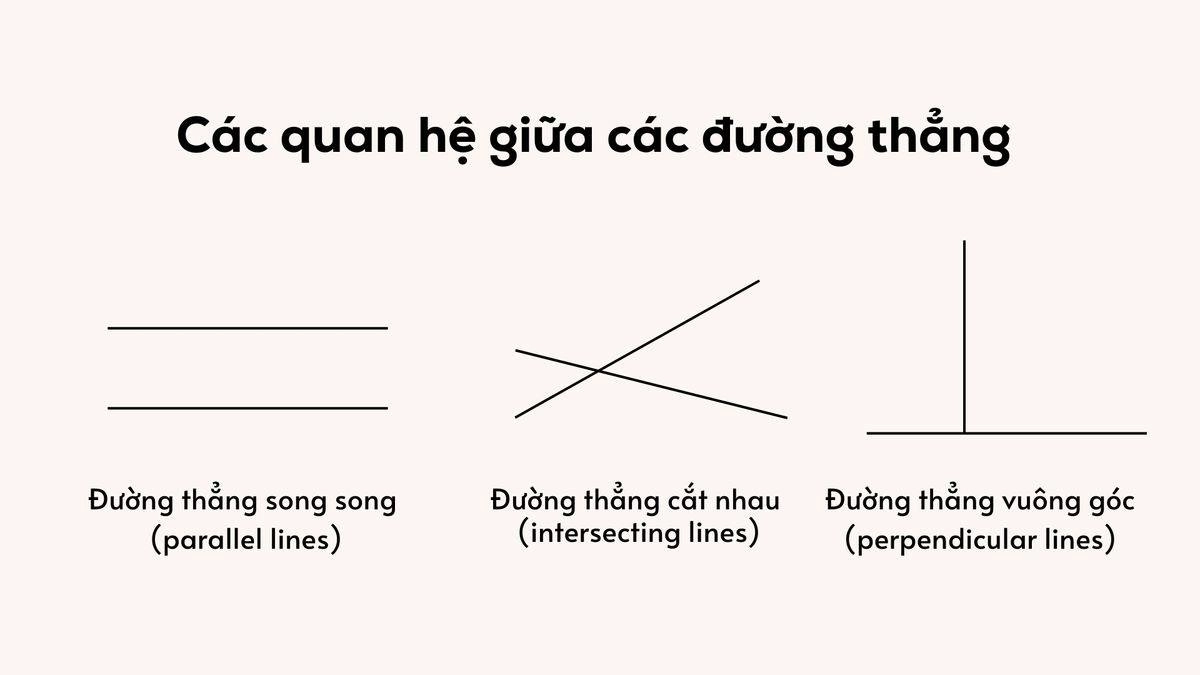
• Đường thẳng song song (parallel lines): Hai đường thẳng được gọi là song song nếu cùng nằm trong một mặt phẳng nhưng không có điểm chung. Dù kéo dài vô hạn về hai phía, chúng không bao giờ gặp nhau, và khoảng cách giữa chúng luôn không đổi. Ký hiệu: d1||d2

• Đường thẳng vuông góc (perpendicular lines): Hai đường thẳng được gọi là vuông góc nếu chúng cắt nhau tại một điểm và góc tạo thành là 90 độ. Ký hiệu: d1⊥d2. Đây là một quan hệ đặc biệt của đường thẳng cắt nhau.

• Đường thẳng cắt nhau (intersecting lines): Hai đường thẳng được gọi là cắt nhau nếu chúng giao nhau tại đúng một điểm, với góc tạo thành lớn hơn 0 độ và bé hơn 180 độ.

Tìm hiểu thêm: Tổng hợp từ vựng SAT Math theo chủ đề

Các loại góc tạo thành khi đường cắt ngang (transversal) cắt hai đường song song

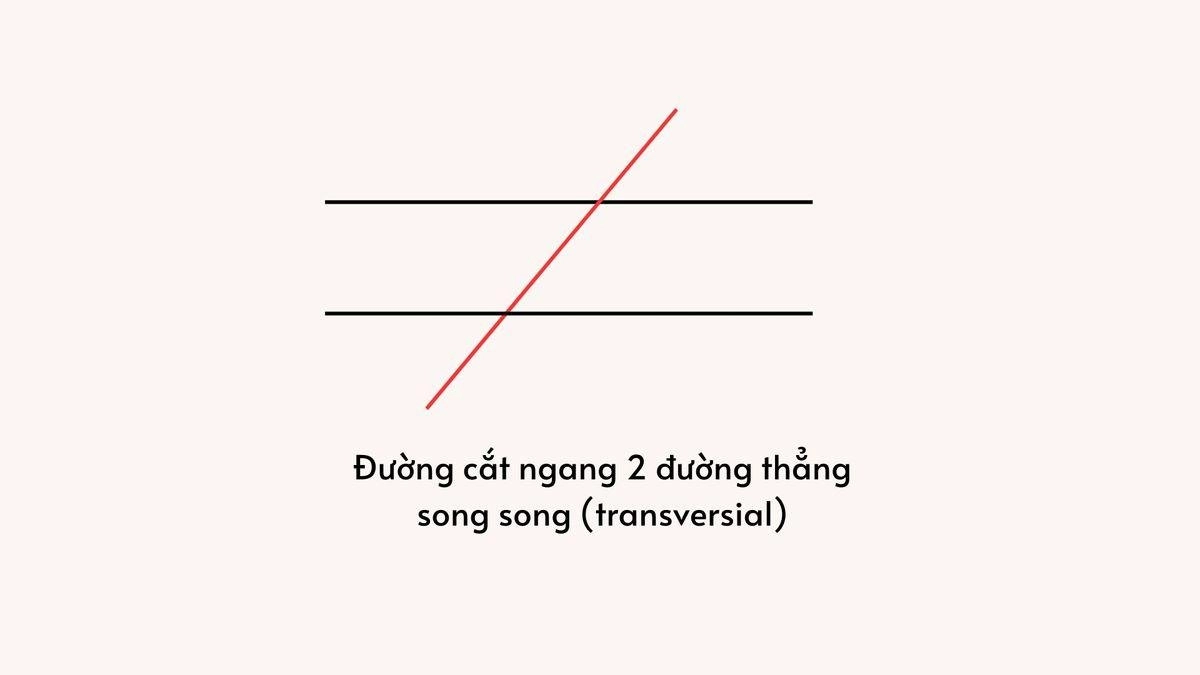
Trong hình học, một đường cắt ngang (transversal) là đường thẳng cắt qua hai hay nhiều đường thẳng khác tại những điểm khác nhau.

Khi đường cắt ngang đi qua hai đường song song, nó tạo nên tám góc tại hai giao điểm. Các góc này không ngẫu nhiên mà tuân theo những quy luật hình học chặt chẽ, được sử dụng rộng rãi trong chứng minh, tính toán và các bài thi chuẩn hóa như SAT.

Từ tình huống trên, ta có thể phân loại các góc thành các nhóm sau:

• Góc đồng vị (Corresponding angles): Là các cặp góc nằm cùng phía của đường cắt ngang và ở vị trí tương tự tại hai giao điểm (ví dụ: trên–trái ở điểm cắt thứ nhất và trên–trái ở điểm cắt thứ hai).

• Góc so le trong (Alternate interior angles): Là các cặp góc nằm giữa hai đường song song nhưng ở hai phía đối nhau của đường cắt ngang.

• Góc trong cùng phía (Consecutive interior angles): Là các cặp góc nằm bên trong hai đường song song và cùng phía của đường cắt ngang.

• Góc ngoài cùng phía (Consecutive exterior angles): Là các cặp góc nằm ngoài hai đường song song và cùng phía của đường cắt ngang.

• Góc đối đỉnh (Vertically opposite angles): Là các cặp góc đối diện nhau khi hai đường thẳng cắt nhau tại một điểm. Các góc này xuất hiện tại từng giao điểm và luôn bằng nhau.

Khi một đường cắt ngang đi qua hai đường song song, các góc hình thành tuân theo các tính chất sau:

• Các góc đồng vị bằng nhau.

• Các góc so le trong bằng nhau.

• Các góc trong cùng phía bù nhau, tức có tổng bằng 180 độ.

• Các góc ngoài cùng phía cũng bù nhau theo nguyên lý tương tự.

• Ngoài ra, các góc đối đỉnh luôn bằng nhau trong mọi trường hợp, không phụ thuộc vào song song hay không.

Những quy tắc này là công cụ cơ bản để giải các dạng toán chứng minh góc, thiết lập phương trình đại số, và suy luận trong các bài SAT. Việc ghi nhớ hệ thống và luyện tập thường xuyên giúp người học tránh nhầm lẫn, đồng thời rút ngắn thời gian giải quyết bài tập.

Các định lý và cách chứng minh liên quan đến đường song song (parallel lines) và đường cắt ngang

Một trong những định lý quan trọng nhất của hình học phẳng là: Nếu một đường cắt ngang cắt hai đường thẳng và tạo ra một cặp góc đồng vị bằng nhau, thì hai đường thẳng đó song song.

Ngược lại, nếu hai đường thẳng song song bị cắt bởi một đường cắt ngang, thì các góc đồng vị tạo thành luôn bằng nhau. Định lý này cung cấp công cụ nền tảng để chứng minh song song cũng như tính toán góc trong nhiều dạng bài.

Có nhiều phương pháp để chứng minh hai đường thẳng song song, trong đó thông dụng nhất gồm:

• Dựa vào các góc đồng vị bằng nhau.

• Dựa vào các góc so le trong bằng nhau.

• Dựa vào các góc trong cùng phía bù nhau.

Mỗi phương pháp đều quy về mối quan hệ góc được tạo bởi một đường cắt ngang, từ đó suy luận song song một cách chặt chẽ.

Ứng dụng định lý trong chứng minh và tính toán:

• Trong chứng minh hình học: Các định lý giúp xác lập song song của các cạnh trong tam giác, hình thang, hay tứ giác đặc biệt.

• Trong tính toán: Việc áp dụng các quan hệ góc đồng vị, so le trong hoặc bù nhau cho phép thiết lập phương trình, giải nhanh giá trị các góc trong đề thi SAT.

Như vậy, nắm chắc các định lý không chỉ hỗ trợ tư duy hình học mà còn cải thiện tốc độ xử lý bài tập trắc nghiệm.

Những lỗi thường gặp khi học về đường cắt ngang và các góc tạo thành

Nhầm lẫn giữa các loại góc

Đây là lỗi phổ biến nhất. Nhiều người học hay nhầm góc đồng vị với góc so le trong, hoặc nhầm giữa góc trong cùng phía và góc ngoài cùng phía.

Nguyên nhân thường do không quan sát kỹ vị trí của các góc so với đường cắt ngang và hai đường song song. Ví dụ, người học dễ tưởng rằng hai góc ở cùng phía nhưng thực tế lại nằm ở vị trí so le.

Không xác định rõ đường cắt ngang

Trong một hình vẽ có nhiều đường, người học thường bị rối và không xác định được đâu là đường cắt ngang chính. Việc xác định sai dẫn đến hệ quả là phân loại sai toàn bộ các cặp góc liên quan.

Quên tính chất đặc biệt khi hai đường song song

Một lỗi nữa là người học nhớ được tên các loại góc nhưng lại quên tính chất của chúng khi hai đường thẳng là song song. Ví dụ, người học biết thế nào là góc đồng vị nhưng không áp dụng được định lý góc đồng vị bằng nhau để giải bài tập chứng minh hoặc tính toán.

Áp dụng sai tính chất trong bài tập

Một số người học áp dụng tính chất trong tình huống không phù hợp, chẳng hạn cho rằng hai góc đồng vị luôn bằng nhau ngay cả khi hai đường thẳng chưa chắc song song. Điều này dẫn đến sai lầm trong chứng minh và giải toán.

Không phân biệt được góc trong và góc ngoài

Khi đường cắt ngang cắt hai đường thẳng, các góc được chia thành “góc trong” (nằm giữa hai đường thẳng) và “góc ngoài” (nằm phía ngoài). Người học thường nhầm lẫn hai khái niệm này, đặc biệt khi hình vẽ phức tạp hoặc đường cắt ngang có nhiều đoạn kéo dài.

Thiếu kỹ năng vẽ hình chính xác

Một số người học vẽ hình không đúng tỉ lệ, hoặc không kẻ đủ đường kéo dài, khiến việc nhận diện các góc trở nên khó khăn. Khi hình vẽ sai, việc suy luận các tính chất dễ dẫn đến kết quả sai.

Không luyện tập đủ dạng bài tập

Có người học chỉ nhớ lý thuyết một cách máy móc mà chưa rèn luyện nhiều bài tập áp dụng, nên khi gặp bài chứng minh quan hệ góc hoặc bài toán có số đo cụ thể thì lúng túng, dễ áp dụng nhầm định lý.

Kỹ thuật giải nhanh các bài toán về parallel lines và transversals trong kỳ thi SAT

Trong kỳ thi SAT, đặc biệt là phần Toán, các câu hỏi về đường song song và đường cắt ngang (transversal) thường xuất hiện dưới dạng trắc nghiệm. Người học cần nắm chắc một số kỹ thuật để giải nhanh:

• Kỹ thuật nhận diện nhanh các góc: Khi gặp bài toán, hãy quan sát ngay vị trí của đường cắt ngang và xác định các cặp góc đồng vị, so le trong, trong cùng phía. Đây là bước quan trọng để quyết định áp dụng tính chất nào.

• Sử dụng sơ đồ và ký hiệu: Người học nên gạch chéo, đánh dấu bằng ký hiệu (ví dụ: dấu bằng hoặc chữ cái A, B, C…) lên hình để phân biệt các góc. Điều này giúp tránh nhầm lẫn giữa các cặp góc, đặc biệt khi hình vẽ có nhiều đường.

• Thiết lập phương trình góc: Với các bài toán yêu cầu tính số đo góc, hãy dựa vào tính chất: góc đồng vị bằng nhau, góc so le trong bằng nhau, góc trong cùng phía bù nhau. Việc chuyển các quan hệ góc thành phương trình đại số giúp người học giải nhanh và chính xác.

Xem thêm:

• Congruence, similarity, and angle relationships - Cách làm và bài tập

• Cách làm dạng bài Geometry and Trigonometry trong SAT Math & Bài tập

• Coordinate Geometry - Dạng toán Hình học tọa độ trong SAT Math

Bài tập vận dụng

Câu 1. Two parallel lines are cut by a transversal. If one of the corresponding angles is 120 degrees, what is the measure of the adjacent interior angle on the same side of the transversal?
A. 60 degrees
B. 120 degrees
C. 150 degrees
D. 180 degrees

Lời giải:
Khi hai đường song song bị cắt bởi một đường cắt ngang, same-side interior angles (góc trong cùng phía) bù nhau.
Nếu một góc bằng 120 độ, thì góc kề trong cùng phía sẽ bằng:
180-120= 60 độ.
→ Đáp án: A.

Câu 2. In the figure, AB||CD, and transversal EF intersects them. If ∠x=3y and ∠y=30 degrees, what is the value of ∠x?
A. 60
B. 75
C. 90
D. 100

Lời giải:
Ta có ∠x=3y. Với ∠y=30 độ, suy ra ∠x=3×30∘=90 độ.
→ Đáp án: C.

Câu 3. A transversal intersects two parallel lines, forming one exterior angle of 70 degrees. What is the measure of the alternate exterior angle?
A. 70°
B. 110°
C. 120°
D. 90°

Lời giải:
Khi hai đường song song bị cắt, alternate exterior angles (góc so le ngoài) bằng nhau.
Do đó, góc đối ứng với 70 độ cũng bằng 70 độ.
→ Đáp án: A.

Tổng kết

Như vậy, bài viết đã giới thiệu về định nghĩa và tính chất của hai đường thẳng song song cũng như là các góc được tạo thành khi có một đường thẳng thứ ba cắt hai đường song song này. Việc luyện tập thường xuyên sẽ giúp người học phản xạ nhanh với các dạng câu hỏi có vận dụng kiến thức về parallel lines - đường thẳng song song - để đạt được thành tích cao trong các bài kiểm tra.

Ngoài ra, để nâng cao kỹ năng làm toán trong bài thi SAT nói riêng và kỹ năng làm bài thi SAT cả hai phần thi Math và Reading and Writing, người học có thể tham khảo các khóa học SAT tại ZIM Academy.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.