Sampling Bias là gì? Chiến lược xử lý trong SAT Math và bài tập
Key takeaways
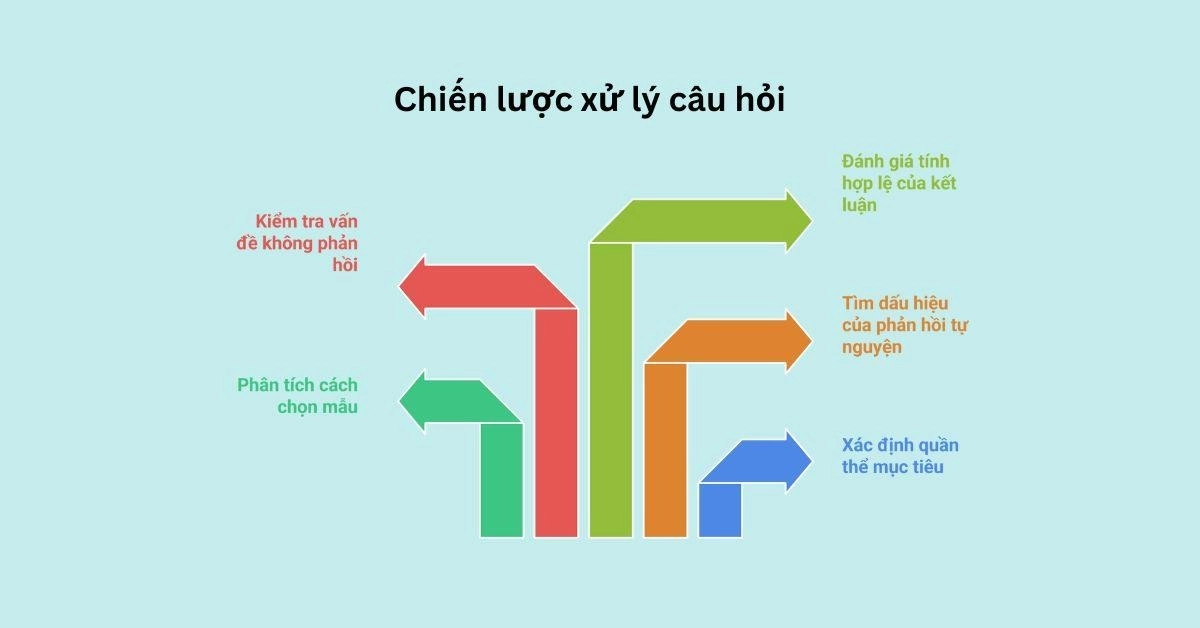
Chiến lược xử lý câu hỏi liên quan đến sampling bias trong SAT Math:
Xác định quần thể mục tiêu
Phân tích cách chọn mẫu
Tìm dấu hiệu của phản hồi tự nguyện
Kiểm tra vấn đề không phản hồi
Đánh giá tính hợp lệ của kết luận
Trong SAT Math, việc nhận diện và hiểu các loại sai lệch trong lấy mẫu rất quan trọng vì nó giúp học sinh đánh giá tính hợp lệ của khảo sát và kết luận đưa ra. Nếu không phát hiện được sai lệch, học sinh có thể chọn đáp án sai do tin vào dữ liệu không đại diện. Kỹ năng này không chỉ nâng cao điểm số mà còn rèn luyện tư duy thống kê thực tiễn. Vì vậy, bài viết dưới đây sẽ trình bày tác động của sampling bias lên kết quả thống kê và sai số phân tích, đồng thời cung cấp chiến lược xử lý câu hỏi dạng này, giúp học sinh nâng cao kỹ năng đánh giá độ tin cậy của dữ liệu để đạt điểm SAT Math cao.
Khái niệm sampling bias và vai trò trong phân tích dữ liệu SAT Math
Sampling bias là gì?
Sampling bias (sai lệch trong lấy mẫu) là hiện tượng xảy ra khi cách chọn mẫu trong một nghiên cứu hoặc khảo sát không phản ánh chính xác đặc điểm của toàn bộ quần thể. Nói cách khác, mẫu bị thiên lệch vì một số nhóm trong quần thể có nhiều khả năng được chọn hơn, hoặc một số nhóm khác bị bỏ sót hoàn toàn. Kết quả là dữ liệu thu thập không đại diện, làm giảm tính chính xác và khách quan của các phân tích thống kê.
Vai trò của Sampling bias trong phân tích dữ liệu SAT Math
Trong phân tích dữ liệu, đặc biệt là trong bối cảnh các bài tập SAT Math, tính đại diện của mẫu là yếu tố then chốt. Nếu mẫu bị sai lệch, các chỉ số thống kê như trung bình, tỷ lệ, hoặc độ lệch chuẩn sẽ không phản ánh đúng thực tế. Ví dụ, nếu muốn khảo sát mức độ hài lòng của học sinh toàn trường về bữa ăn trưa nhưng chỉ chọn mẫu từ học sinh thường xuyên ăn tại căn tin, kết quả sẽ thiên về nhóm này và không thể đại diện cho tất cả học sinh.
Trong SAT Math, học sinh thường được yêu cầu xác định xem một khảo sát hoặc thí nghiệm có hợp lệ không. Khả năng nhận biết sampling bias giúp thí sinh phân tích chính xác tình huống, phát hiện sự thiên lệch trong thiết kế mẫu, và từ đó chọn đáp án đúng. Đây không chỉ là kỹ năng làm bài thi mà còn là năng lực tư duy thống kê quan trọng trong thực tiễn nghiên cứu và đời sống.
Đọc thêm: Cách làm dạng Evaluating statistical claims trong SAT Math và bài tập
Những loại sai lệch thường gặp trong lấy mẫu (sampling bias)
Trong SAT Math, học sinh thường gặp những câu hỏi về khảo sát hoặc thí nghiệm mà việc nhận diện sai lệch là chìa khóa để chọn đáp án đúng. Dưới đây là các dạng sai lệch phổ biến.
Selection bias (sai lệch lựa chọn mẫu)
Đây là loại sai lệch diễn ra khi cách chọn mẫu khiến cho một nhóm đối tượng có nhiều khả năng được chọn hơn các nhóm khác, làm mẫu không đại diện. Ví dụ: một trường muốn khảo sát thói quen đọc sách của học sinh nhưng chỉ chọn mẫu từ thư viện. Rõ ràng, nhóm này có xu hướng đọc nhiều sách hơn trung bình toàn trường.
Voluntary response bias (sai lệch phản hồi tự nguyện)
Xảy ra khi khảo sát dựa trên việc người tham gia tự nguyện phản hồi, thường dẫn đến sự mất cân bằng. Những người có ý kiến mạnh mẽ, tích cực hoặc tiêu cực, thường phản hồi nhiều hơn. Ví dụ: một tờ báo online mở bình chọn về việc tăng học phí, chỉ những phụ huynh quan tâm hoặc bất mãn mới tham gia. Kết quả khảo sát không thể đại diện cho toàn bộ phụ huynh.
Non-response bias (sai lệch không phản hồi)
Sai lệch này xảy ra khi một tỷ lệ lớn những người được chọn không phản hồi, và những người không trả lời có đặc điểm khác biệt với nhóm trả lời. Ví dụ: một khảo sát gửi email đến toàn bộ sinh viên về mức độ căng thẳng, nhưng phần lớn người quá bận rộn hoặc căng thẳng lại không trả lời. Như vậy sẽ dẫn đến kết quả của khảo sát nghiêng về nhóm ít căng thẳng hơn thực tế.
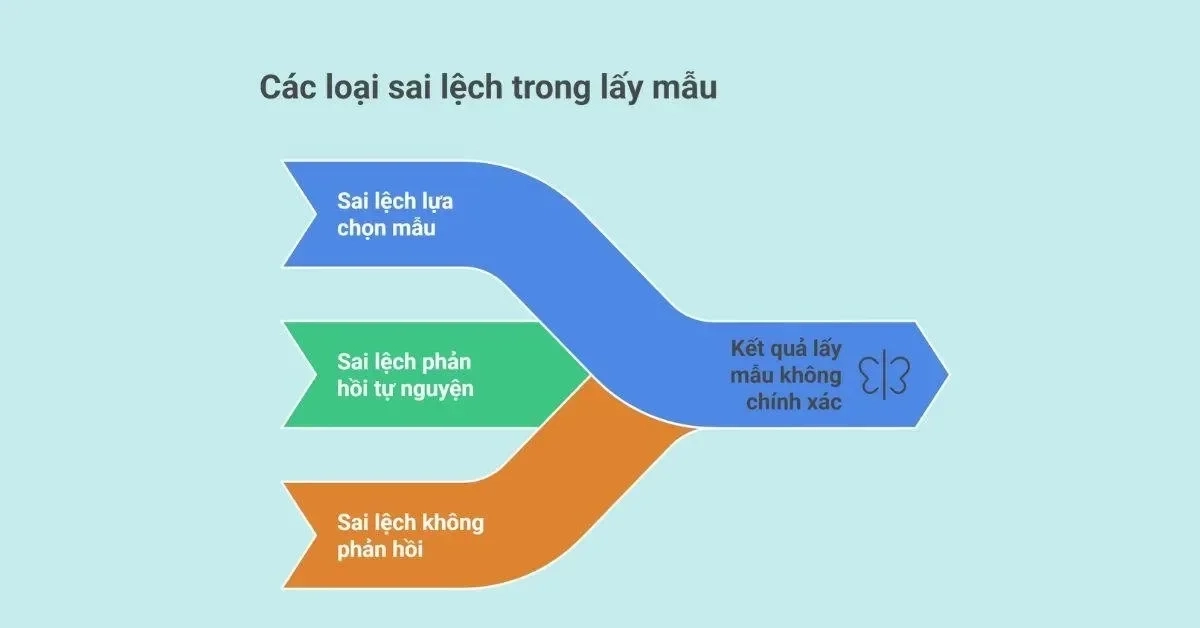
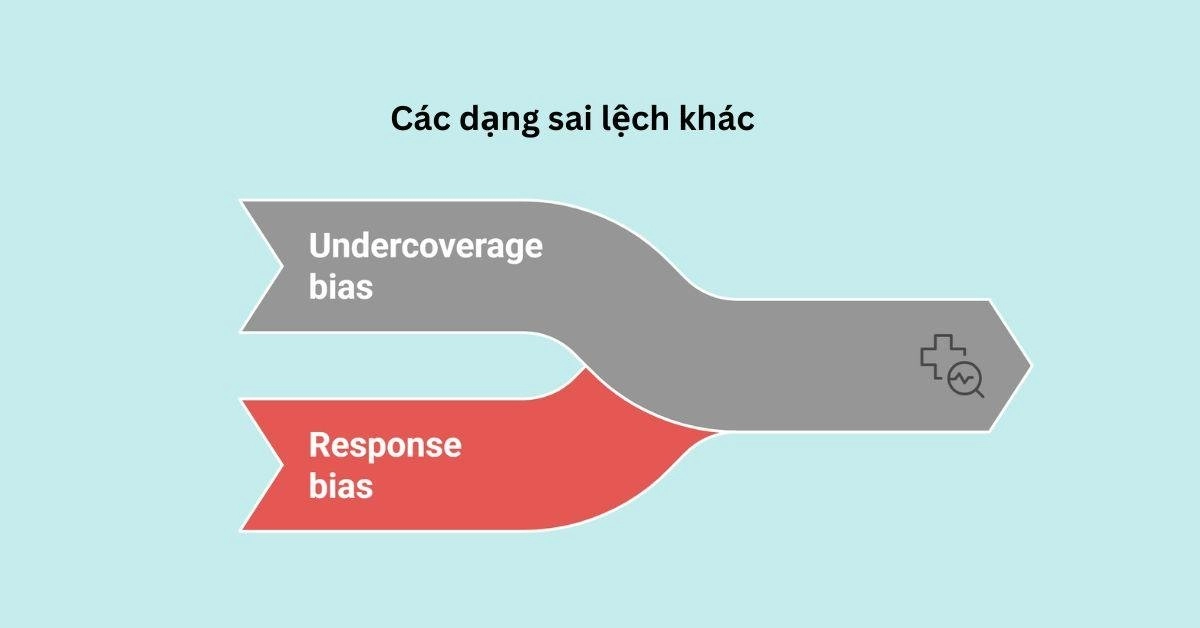
Các dạng sai lệch khác
Undercoverage bias (thiếu bao quát): Xảy ra khi một nhóm trong quần thể không có cơ hội được chọn vào mẫu. Ví dụ: một công ty muốn khảo sát mức độ hài lòng của khách hàng với dịch vụ giao hàng trực tuyến. Tuy nhiên, họ chỉ phát phiếu khảo sát tại các cửa hàng trực tiếp của công ty. Điều này loại bỏ toàn bộ nhóm khách hàng chỉ mua hàng online mà không bao giờ đến cửa hàng, khiến mẫu không phản ánh đúng toàn bộ quần thể khách hàng.
Response bias (sai lệch phản hồi): Người tham gia không đưa ra câu trả lời trung thực do câu hỏi mang tính nhạy cảm. Ví dụ: khảo sát học sinh về việc gian lận trong thi cử, nhiều em sẽ trả lời “không” dù thực tế có gian lận.
Tìm hiểu thêm: Essential Vocab for SAT® Math - Problem Solving and Data Analysis | Unit 4: Biased and Unbiased
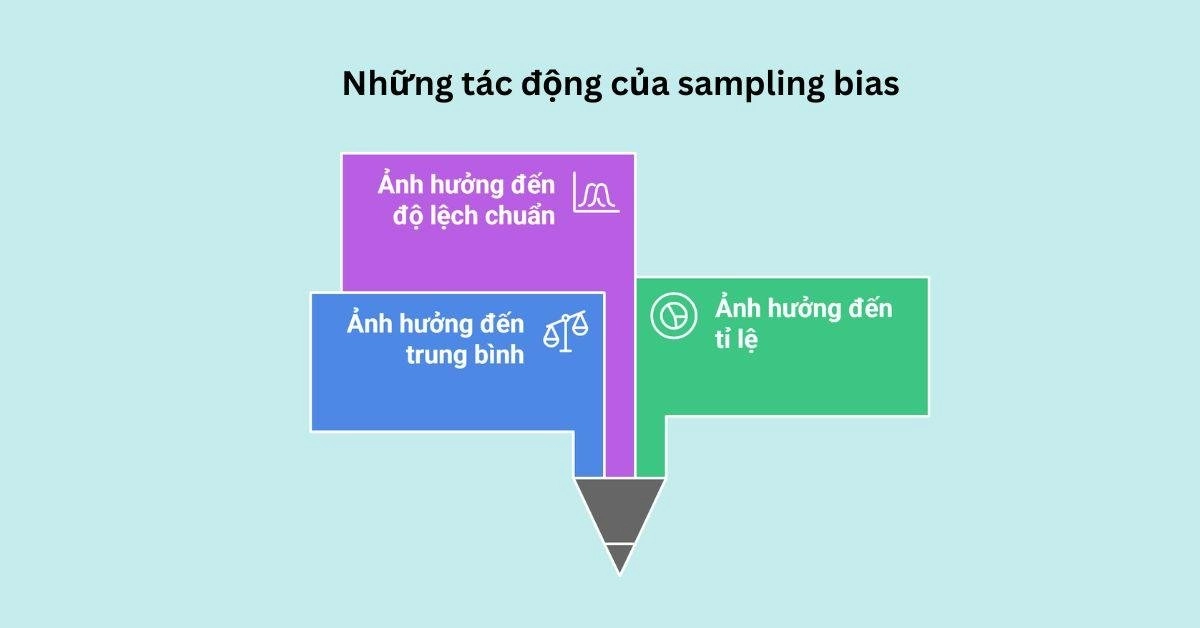
Những tác động của sampling bias lên kết quả thống kê và sai số phân tích
Sampling bias (sai lệch lấy mẫu) có ảnh hưởng trực tiếp đến độ chính xác của các phép đo thống kê như trung bình (mean), tỉ lệ (proportion), và độ lệch chuẩn (standard deviation). Khi mẫu không đại diện cho quần thể, các thống kê mô tả từ mẫu không phản ánh đúng thực tế, dẫn đến sai lầm trong kết luận.
Ảnh hưởng đến trung bình (mean)
Nếu mẫu thiên về một nhóm có giá trị cao hoặc thấp hơn so với mặt bằng chung, giá trị trung bình của mẫu sẽ bị dịch chuyển. Ví dụ, khảo sát thu nhập trung bình của cư dân thành phố nhưng chỉ chọn người ở khu phố giàu có, kết quả sẽ cao hơn nhiều so với thực tế. Sai lệch này khiến người phân tích đưa ra dự đoán sai lệch về mức sống chung.
Ảnh hưởng đến tỉ lệ (proportion)
Trong trường hợp nghiên cứu ý kiến hoặc hành vi, sai lệch mẫu có thể làm thay đổi tỷ lệ phần trăm đáng kể. Chẳng hạn, khảo sát ý kiến về việc mở thêm phòng tập thể thao nhưng chỉ hỏi những người đang ở phòng gym sẽ cho tỉ lệ ủng hộ cao hơn nhiều so với toàn bộ dân cư. Kết luận từ dữ liệu như vậy sẽ dẫn đến quyết định sai lầm trong hoạch định chính sách.
Ảnh hưởng đến độ lệch chuẩn (standard deviation)
Độ lệch chuẩn phản ánh mức độ phân tán dữ liệu. Nếu mẫu chỉ bao gồm những cá thể có đặc điểm tương tự nhau (ví dụ: học sinh trong một lớp chọn toàn học sinh giỏi), độ lệch chuẩn sẽ thấp bất thường. Điều này tạo ra ảo giác rằng sự khác biệt trong quần thể nhỏ hơn thực tế.
Chiến lược xử lý câu hỏi liên quan đến sampling bias trong SAT Math
Trong SAT Math, dạng câu hỏi về sampling bias (sai lệch lấy mẫu) thường xuất hiện dưới dạng phân tích khảo sát, thí nghiệm, hoặc nghiên cứu thống kê. Nhiệm vụ của thí sinh là nhận diện xem mẫu được lấy có đại diện cho toàn bộ quần thể hay không, và từ đó đánh giá tính hợp lệ của kết luận. Để làm tốt dạng này, học sinh có thể áp dụng chiến lược sau:
Xác định quần thể mục tiêu
Bước đầu tiên là tìm hiểu khảo sát hoặc thí nghiệm muốn đưa ra kết luận cho nhóm đối tượng nào. Ví dụ, nếu đề nói “toàn bộ cư dân thành phố”, nhưng mẫu chỉ thu thập từ người sống gần một công viên, thì ngay lập tức có dấu hiệu sai lệch.
Phân tích cách chọn mẫu
Đọc kỹ mô tả: khảo sát thực hiện ở đâu, bằng cách nào, với ai. Đây là điểm mấu chốt để phát hiện selection bias (sai lệch lựa chọn mẫu). Ví dụ: khảo sát về thực đơn mới nhưng chỉ thực hiện ở quầy salad sẽ dẫn đến kết quả thiên lệch.
Tìm dấu hiệu của phản hồi tự nguyện
Nếu khảo sát dựa trên việc người tham gia tự nguyện trả lời (online poll, liên kết website, email mời), thì khả năng cao rơi vào voluntary response bias – vì những người quan tâm mạnh mẽ sẽ có xu hướng phản hồi nhiều hơn.
Kiểm tra vấn đề không phản hồi
Học sinh có thể đặt câu hỏi: Có nhóm nào trong quần thể bị bỏ sót không? Ví dụ, khảo sát bằng bưu thiếp chỉ in tiếng Anh sẽ bỏ qua cư dân không rành tiếng Anh, gây ra undercoverage bias.
Đánh giá tính hợp lệ của kết luận
Khi mẫu không đại diện, kết luận rút ra sẽ thiếu chính xác hoặc thổi phồng một xu hướng nào đó. Trong SAT, nếu câu hỏi yêu cầu chọn lý do “làm yếu” hay “ít làm yếu nhất” kết luận, hãy cân nhắc xem chi tiết nào thực sự ảnh hưởng đến tính đại diện.
Chiến lược trả lời nhanh
Tìm mấu chốt trong cách chọn mẫu.
Gạch chân những chi tiết gây thiên lệch (địa điểm, phương pháp, ngôn ngữ, hình thức tự nguyện).
So sánh xem mẫu có phản ánh toàn bộ quần thể hay không.
Loại trừ đáp án không liên quan đến vấn đề đại diện.
Đọc thêm: Giải thích dữ liệu từ biểu đồ và bảng phức tạp trong SAT Math
Bài tập vận dụng
Bài tập 1.
The city plans to build a skatepark downtown. A survey of 220 people was conducted at an upscale gym near the proposed site, and the results showed that 62% opposed the plan. Which of the following most likely explains why the percentage of opposition is higher than it would be for the city as a whole?
(A) The sample was taken at an upscale gym near the site.
(B) The city used random phone calls throughout the city.
(C) The sample size of 220 was small.
(D) The survey was conducted over 3 days, including a weekend.
Bài tập 2.
An ice rink conducted an open poll on its hockey team’s fan page and concluded that “the majority of respondents want later opening hours.” What is the main source of bias?
(A) Voluntary response/self-selection bias, since only those following the fan page and motivated to vote participated.
(B) The survey did not report a margin of error.
(C) The sample size was 4,500.
(D) The percentages were rounded.
Bài tập 3.
A transit agency wanted to measure satisfaction among all bus riders. They distributed questionnaires on buses during weekdays from 7–9 a.m., and concluded that 82% of riders were satisfied. Which of the following best describes a limitation of the survey?
(A) The sample included only weekday morning riders, not those who ride at other times.
(B) The survey was randomly conducted across all routes throughout the day.
(C) The questionnaires were anonymous.
(D) The survey lasted for 2 weeks.
Bài tập 4.
A city is considering opening a community tutoring center near High School A. A research company surveyed 180 students from High School A, and 74% supported the proposal. Which of the following, if true, would LEAST invalidate this conclusion?
(A) Most respondents lived within walking distance of the proposed center.
(B) The survey was conducted during lunchtime in the school’s STEM wing.
(C) Respondents were all students from High School A across different grade levels.
(D) Data was collected within 2 weeks after the proposal was announced.
Bài tập 5.
A city wants to measure support for stricter noise regulations around an outdoor performance stage. Officials mailed postcards with the survey to residents living within 2 miles of the stage and also posted a survey link on the stage’s website. There were 1,200 responses, with 55% in favor. Which of the following, if true, would LEAST weaken the conclusion that a slim majority of residents support the proposal?
(A) The postcards were printed only in English, excluding residents who are not fluent in English.
(B) A large proportion of responses came from the survey link on the stage’s website.
(C) The mailing list of postcards did not include residents who moved in within the last six months.
(D) The results were weighted by age and location to match the overall population of the city.
Đáp án
Bài tập 1.
Đáp án: (A)
Phân tích:
Quần thể mục tiêu: cư dân toàn thành phố.
Cách lấy mẫu: người tập ở phòng gym cao cấp, lại gần địa điểm ⇒ nhóm bị ảnh hưởng trực tiếp (ồn ào, đông người) và có đặc điểm KT-XH khác.
Sai lệch: selection bias → khuynh hướng phản đối cao hơn mức chung.
(B) là phương pháp tốt (ngẫu nhiên); (C) là sai số ngẫu nhiên, không tạo thiên lệch có hướng; (D) không gợi sai lệch hệ thống.
Bài tập 2.
Đáp án: (A)
Phân tích:
Quần thể mục tiêu: khách sân băng nói chung.
Mẫu: người theo dõi fanpage + tự nguyện bấm phiếu ⇒ selection + voluntary response bias.
(B)(C)(D) không phải nguồn sai lệch hệ thống.
Bài tập 3.
Đáp án: (A)
Phân tích:
Quần thể mục tiêu: tất cả hành khách (sáng/chiều/tối, cuối tuần).
Mẫu: khung giờ hẹp ⇒ bỏ sót học sinh, ca đêm, cuối tuần…
Sai lệch: undercoverage/selection theo thời gian.
(B) là phương pháp tốt, (C)(D) không gây bias đại diện.
Bài tập 4.
Đáp án: (D)
Phân tích:
Quần thể mục tiêu: cư dân thành phố.
Mẫu: chỉ học sinh trường A ⇒ thiên về nhóm hưởng lợi trực tiếp.
(A) và (B) làm selection bias nặng hơn; (C) mở rộng trong cùng một cụm nên vẫn thiên lệch.
(D) chỉ nói về thời gian thu thập ngắn, không tạo thiên lệch đại diện ⇒ ít làm suy yếu nhất.
Bài tập 5.
Đáp án: (D)
Phân tích:
Quần thể mục tiêu: cư dân toàn thành phố (không chỉ trong bán kính 2 dặm, không chỉ người truy cập trang web).
Mẫu thực tế: cư dân gần khu vực + người tự nguyện trên website ⇒ nguy cơ undercoverage (cư dân xa hơn) và voluntary response bias (người quan tâm/khán giả).
(A) Tạo undercoverage theo ngôn ngữ ⇒ làm suy yếu.
(B) Tăng voluntary response bias từ fan của sân khấu ⇒ làm suy yếu.
(C) Undercoverage cư dân mới ⇒ làm suy yếu.
(D) Gán trọng số để khớp cấu trúc dân số toàn thành phố là bước hiệu chỉnh giúp giảm thiên lệch ⇒ ít làm suy yếu nhất.
Ôn tập thêm: Cách làm dạng bài Problem Solving and Data Analysis trong SAT Math
Tổng kết
Bài viết trên đã giải thích các loại sai sampling bias (lệch trong lấy mẫu) và tác động của chúng đến tính đại diện của mẫu trong SAT Math. Việc thành thạo nhận diện và đánh giá sampling bias có một vai trò quan trọng trong SAT Math vì nó thường xuất hiện trong các câu hỏi về khảo sát và dữ liệu thống kê. Kỹ năng này giúp thí sinh nhanh chóng phát hiện sai lệch trong thiết kế mẫu, từ đó lựa chọn đáp án chính xác và tránh các bẫy thường gặp. Quan trọng hơn, nó còn phản ánh tư duy phân tích logic và khả năng xử lý thông tin — những kĩ năng được các trường đại học danh tiếng đánh giá cao, góp phần nâng cao điểm số và cơ hội trúng tuyển.
Bên cạnh đó, thí sinh có thể tham khảo khoá học luyện thi SAT tại ZIM Academy.
Nguồn tham khảo
“Evaluating statistical claims | Lesson.” Khan Academy, 15/08/2025. https://www.khanacademy.org/test-prep/v2-sat-math/x0fcc98a58ba3bea7:problem-solving-and-data-analysis-easier/x0fcc98a58ba3bea7:evaluating-statistical-claims-easier/a/v2-sat-lesson-evaluating-statistical-claims. Accessed 15 August 2025.

Bình luận - Hỏi đáp