Essential vocabulary for SAT® Math - Advanced Math | Unit 6: Growth and Decay

Trong SAT Math, nhiều bài toán đề cập đến sự thay đổi của một đại lượng. Từ vựng “growth” và “decay” là những khái niệm cơ bản thể hiện sự tăng và giảm đối với dạng bài này. Trong bài viết dưới đây, tác giả sẽ giới thiệu về Essential vocabulary for SAT Math - Advanced Math - Unit 6: growth + decay kèm bài tập vận dụng giúp người học hiểu rõ hơn về hai khái niệm này trong toán học nói chung cũng như trong kỳ thi SAT Math.

Growth (n): sự tăng trưởng

Định nghĩa

Trong toán học, growth (sự tăng trưởng) là sự gia tăng về số lượng, giá trị, mức độ, cường độ,… của một đại lượng theo thời gian.

Ví dụ:

• Dân số Ấn Độ tăng từ khoảng 1,2 tỷ năm 2010 lên hơn 1,4 tỷ vào năm 2025.

• Lượng tiền gửi ngân hàng tăng theo lãi suất kép.

• Số lượng vi khuẩn nhân đôi sau mỗi chu kỳ tăng trưởng.

Công thức

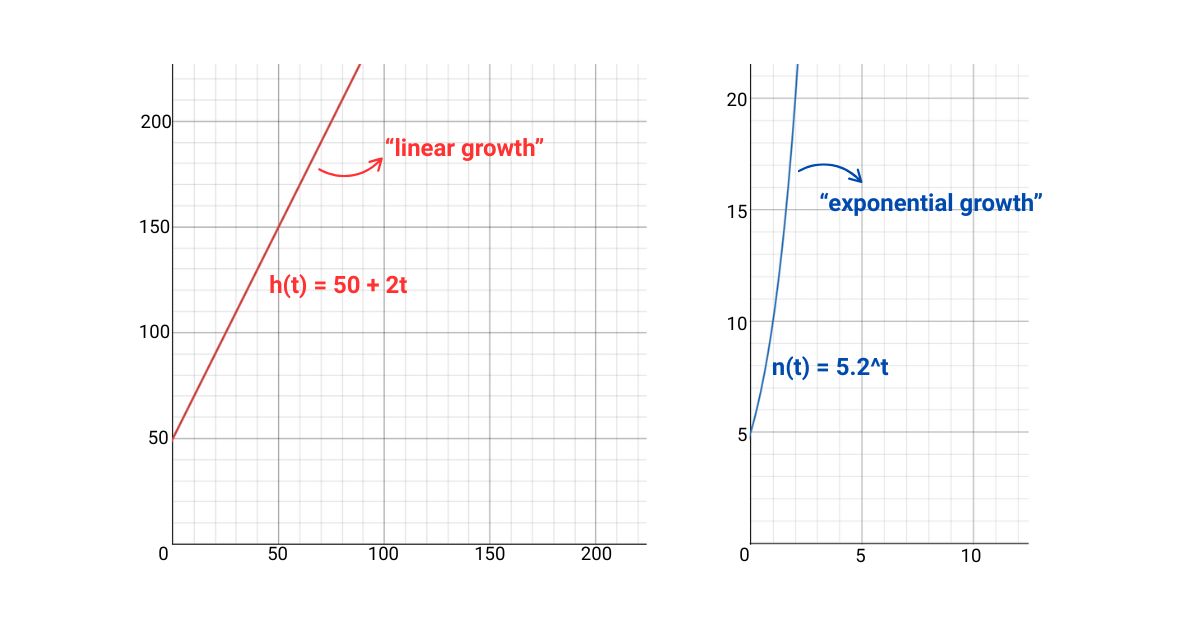
Có hai dạng tăng trưởng chính: tăng trưởng tuyến tính (linear growth), tăng trưởng theo cấp số nhân (exponential growth).

Tăng trưởng tuyến tính:

Trong đó:

• y: giá trị tại thời điểm t

• y0​: giá trị ban đầu

• k: hệ số thay đổi

• t: thời gian

Ví dụ:

Vào thời điểm bắt đầu khảo sát, cây A cao 10 cm, sau mỗi tuần cây tăng thêm 2 cm.

Sự tăng trưởng chiều cao của cây được biểu diễn bằng hàm số sau: h(t) = 50 + 2t.

Tăng trưởng theo cấp số nhân:

Trong đó:

• y: giá trị tại thời điểm t

• y0​: giá trị ban đầu

• k: hệ số thay đổi

• t: thời gian

Ví dụ: Số lượng vi khuẩn ban đầu là 20, sau mỗi giờ, lượng vi khuẩn tăng gấp đôi.

Sự tăng trưởng của vi khuẩn được biểu diễn bằng hàm số sau: \(n\left(t\right)=5\cdot2^{t}\) .

Kiểm tra từ vựng

Fill in the blank with one of these words: increases, exponential, positive

1. The formula for __________ growth is y=a⋅b^t, where b > 1.

2. A linear growth occurs when a value __________ by the same amount per unit time.

3. Linear growth has a __________ slope, meaning the value rises with time.

Bài toán thực tế

Exercise 1:

A software engineer starts her job with a monthly salary of $2,500. Her company offers her a fixed raise of $150 every 6 months.
How much will she earn per month after 4 years?

Exercise 2:

A certain type of bacteria reproduces through exponential growth.
The initial population is 2,000 cells, and it doubles every 3 hours.

a) How many bacteria will there be after 15 hours?
b) After how many hours will the population exceed 128,000?

Xem thêm: Cách làm Advanced Math trong SAT Math

Decay (n): sự suy giảm

Định nghĩa

Trong toán học, decay (sự suy giảm) là sự giảm về số lượng, giá trị, mức độ, cường độ,… của một đại lượng theo thời gian.

Ví dụ:

• Chất phóng xạ như phân rã khiến lượng chất giảm dần theo thời gian.

• Giá trị cổ phiếu công ty A giảm dần sau mỗi quý.

• Một số hormone trong cơ thể giảm dần khi con người trưởng thành.

Công thức

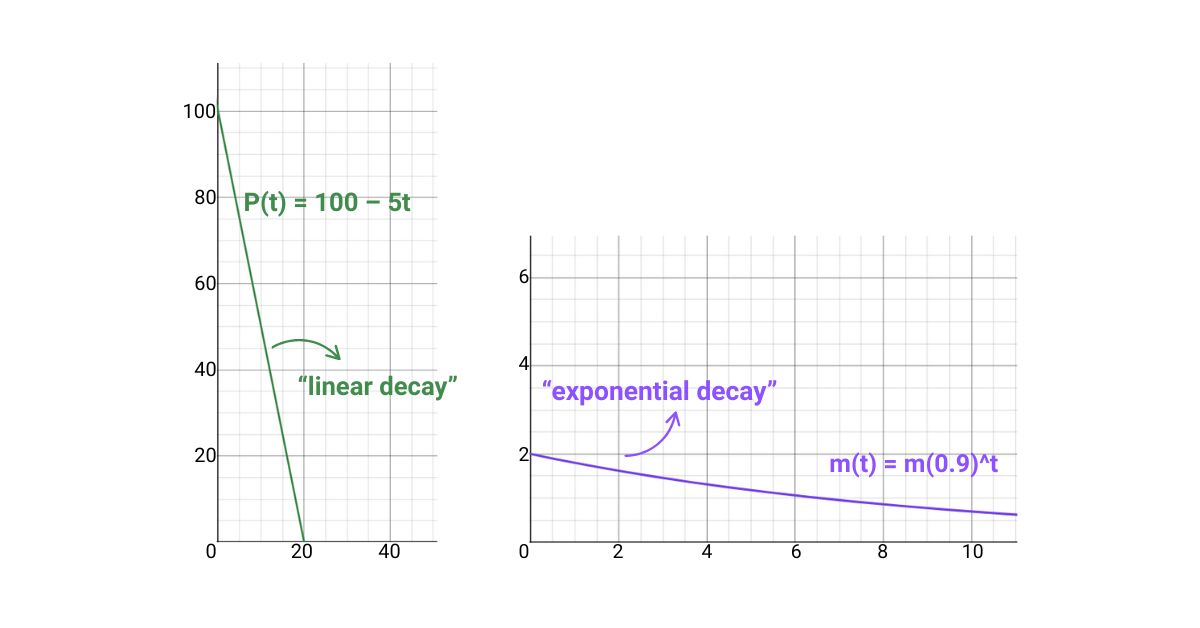
Có hai dạng suy giảm chính: suy giảm tuyến tính (linear decay) và suy giảm theo cấp số nhân (exponential decay). Các công thức thể hiện sự suy giảm tương tự với tăng trưởng nhưng có giá trị hệ số khác.

Suy giảm tuyến tính: \(y=y_0+kt\) (k < 0)

Ví dụ: Pin điện thoại mất đều 5% mỗi giờ. Hàm số thể hiện mức pin là: \(P\left(t\right)=100-5t\).

Suy giảm theo cấp số nhân: \(y=y_0\cdot k^{t}\) (k < 1)

Ví dụ: Một khối chất phóng xạ có khối lượng 2 gram, khối lượng giảm 10% sau mỗi ngày. Công thức thể hiện sự suy giảm khối lượng của chất này là: \(m\left(t\right)=2\cdot0.9^{t}\).

Kiểm tra từ vựng

Fill in the blank with one of these words: downward, decay, exponential

1. Radioactive substances typically follow a pattern of __________ decay over time.

2. The graph of exponential decay forms a __________-sloping curve.

3. In a linear __________ model, the slope of the function is less than zero.

Bài toán thực tế

Exercise 1:

A flashlight uses a battery that drains at a constant rate. Initially, the battery holds 1800 mAh of charge, and it loses 75 mAh per hour when in use.

How many hours will it take for the battery to be completely drained?

Exercise 2:

A radioactive substance weighing 100 grams undergoes exponential decay. Its half-life is 5 years (Radioactive half-life is the time it takes for half of the unstable nuclei in a sample of a radioactive substance to decay.)

a) Write a function M(t) to model the remaining mass after t years.
b) After how many years will only 12.5 grams remain?

Đáp án

Growth

1. The formula for exponential growth is y=a⋅b^t where b>1.
   (Công thức cho sự tăng trưởng theo cấp số nhân là y=a⋅b^t với b>1.)

2. A linear growth occurs when a value increases by the same amount per unit time.
   (Tăng trưởng tuyến tính xảy ra khi một giá trị tăng lên cùng một lượng cố định theo mỗi đơn vị thời gian.)

3. Linear growth has a positive slope, meaning the value rises with time.

   
   (Tăng trưởng tuyến tính có hệ số góc dương, nghĩa là giá trị tăng theo thời gian.)

Exercise 1:

• Starting salary S0 = 2500 USD/month

• Raise every 6 months = 150 USD

• Duration = 4 years = 8 periods of 6 months

The salary increases linearly by $150 every 6 months.
After n = 8, the salary is: S = S0 + 150n = 2500 + 150.8 = 3700 USD/month.

Exercise 2:

• Initial population P0 = 2000 cells

• The population doubles every 3 hours.

• Time in hours

The population doubles every 3 hours means: \(P\left(t\right)=P_0\cdot2^{\frac{t}{3}}\)

a) Number of bacteria after 15 hours: P(15) = 64000 (cells)
b) The population exceed 128,000 after: P(t) > 128000 → t > 18 hours.

Decay

1. Radioactive substances typically follow a pattern of exponential decay over time.
   (Các chất phóng xạ thường tuân theo mô hình suy giảm theo cấp số nhân theo thời gian.)

2. The graph of exponential decay forms a downward-sloping curve.
   (Đồ thị của sự suy giảm theo cấp số nhân tạo thành một đường cong đi xuống.)

3. In a linear decay model, the slope of the function is less than zero.
   (Trong mô hình suy giảm tuyến tính, hệ số góc của hàm số nhỏ hơn không.)

Exercise 1:

• Initial battery charge: 1800 mAh

• Constant loss: 75 mAh/hour

Loss of battery is presented by a linear decay function: B(t) = 1800 — 75t.

The battery is completely drained after: B(t) = 1800 — 75t = 0 → t = 24 hours.

Exercise 2:

• Initial mass: 100 g

• Half-life: 5 years

a) The function follows an exponential decay pattern: \(M\left(t\right)=100\cdot\left(\frac12\right)^{\frac{t}{5}}\).

b) The substance remains 12.5 g after: M(t) = 12.5 → t =15 years.

Bài viết trên đã giới thiệu về Essential vocabulary for SAT Math - Advanced Math - Unit 6: growth + decay. “Growth” chỉ sự tăng trưởng, và “decay” được dùng để nói về sự suy giảm của các đại lượng toán học. Người học cần hiểu rõ hai khái niệm này và cách sử dụng chúng trong bối cảnh toán học nhằm hiểu đúng và làm tốt các bài tập SAT Math. Để xây dựng các kiến thức nền tảng về SAT một cách vững chắc, người học có thể đăng ký khoá học SAT Foundation tại ZIM Academy.

Để đạt kết quả cao trong kỳ thi SAT, việc nắm vững chiến lược và phương pháp giải các dạng toán là yếu tố then chốt. Sách Think in SAT Digital Math - Reasoning and Strategies cung cấp cho thí sinh cái nhìn tổng quan về các dạng toán trong kỳ thi, cùng hướng tư duy hiệu quả để giải quyết từng dạng bài. Mỗi chủ đề được trình bày với kiến thức cơ bản, ví dụ minh họa, cách giải mẫu và bài tập luyện tập kèm đáp án chi tiết.

SAT® is a trademark registered by the College Board, which is not affiliated with, and does not endorse, this website.